Đề kiểm tra giữa học kì 2 - Đề số 3

Trong tam giác $ABC$, ta có.

Cho \(x > 8y > 0.\) Giá trị nhỏ nhất của biểu thức \(F = x + \dfrac{1}{{y\left( {x - 8y} \right)}}\) là:

Tìm giá trị lớn nhất $M$ của hàm số $f\left( x \right) = \left( {6x + 3} \right)\left( {5 - 2x} \right)$ với $x \in \left[ { - \dfrac{1}{2};\dfrac{5}{2}} \right].$

Tập nghiệm \(S\) của hệ bất phương trình $\left\{ \begin{array}{l}\dfrac{{x - 1}}{2} <  - x + 1\\3 + x > \dfrac{{5 - 2x}}{2}\end{array} \right.$ là:

Cho ba điểm A, B, C phân biệt. Điều kiện cần và đủ để ba điểm A, B, C thẳng hàng là:

Cho hai đường thẳng \({d_1}:2x - 4y - 3 = 0\) và \({d_2}:3x - y + 17 = 0\). Số đo góc giữa \({d_1}\) và \({d_2}\) là

Điểm \(A\left( { - 1;3} \right)\) là điểm thuộc miền nghiệm của bất phương trình:

Tập nghiệm của bất phương trình: $-{x^2} + 6x + 7\; \ge 0\;$là:

Gọi \(S\) là tập nghiệm của bất phương trình \( - 2 \le x \le 4\). Chọn mệnh đề đúng:

Tam thức bậc hai \(f\left( x \right) = \left( {1 - \sqrt 2 } \right){x^2} + \left( {5 - 4\sqrt 2 } \right)x - 3\sqrt 2  + 6\)

Bất phương trình $\left| {1 - 3x} \right| > 2$ có nghiệm là

Tam giác \(ABC\) có \(AB = 4,\;BC = 6,\;AC = 2\sqrt 7 \). Điểm \(M\) thuộc đoạn \(BC\) sao cho \(MC = 2MB\). Tính độ dài cạnh \(AM\).  

Tìm điều kiện xác định của bất phương trình $\sqrt {\dfrac{{x + 1}}{{{{\left( {x - 2} \right)}^2}}}}  < x + 1.$

Phương trình đường thẳng đi qua hai điểm \(A\left( { - 2;4} \right)\,;B\left( { - 6;1} \right)\) là:

Cho $f\left( x \right) = {x^2} - 4x + 3$. Trong các mệnh đề sau, mệnh đề đúng là:

Cho tam giác \(ABC\)  có \(\widehat B = {30^0},\widehat C = {105^0}\) và \(AC = 6\). Kết quả nào trong các kết quả sau là độ dài của cạnh \(BC\)?

Bất phương trình $\sqrt {{x^2} - x - 12}  < x$ có tất cả bao nhiêu nghiệm nguyên trên $\left[ { - \,2018;2018} \right]$ ?

Cho \(f\left( x \right) = a{x^2} + bx + c\,\left( {a \ne 0} \right)\). Điều kiện để \(f\left( x \right) \ge 0\,,\,\forall x \in \mathbb{R}\) là

Cho đường thẳng \(\left( d \right):3x + 5y - 15 = 0\). Phương trình nào sau đây không trùng (d).

Giá trị nguyên dương lớn nhất để hàm số $y = \sqrt {5 - 4x - {x^2}} $ xác định là

Đường thẳng \(\left( \Delta \right)\): \(3x - 2y - 7 = 0\) cắt đường thẳng nào sau đây?

Giải bất phương trình \( - 2{x^2} + 3x - 7 \ge 0.\)

Cho biểu thức \(f\left( x \right) = 2x - 4.\) Tập hợp tất cả các giá trị của \(x\) để \(f\left( x \right) \ge 0\) là

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

Cho biểu thức \(f\left( x \right) = \left( {x + 5} \right)\left( {3 - x} \right).\) Tập hợp tất cả các giá trị của \(x\) thỏa mãn bất phương trình \(f\left( x \right) \le 0\) là

Phương trình nào sau đây biểu diễn đường thẳng không song song với đường thẳng \(\left( d \right):\,y = 2x - 1\)?

Cho hai đường thẳng song ${d_1}:5x - 7y + 4 = 0\,\,$và ${d_2}:5x - 7y + 6 = 0.\,\,$Khoảng cách giữa \({d_1}\) và \({d_2}\) là

Trong tam giác \(ABC\) có:

Cho bất phương trình \(2x + 3y - 6 \le 0\,\,(1)\). Chọn khẳng định đúng trong các khẳng định sau

Mệnh đề nào sau đây sai? Đường thẳng \(\left( d \right)\) được xác định khi biết.

Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \({m^2}x - 1 < mx + m\) có nghiệm.

Tập nghiệm của bất phương trình $\dfrac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1$ là

Bất phương trình \(\dfrac{4}{{x - 1}} - \dfrac{2}{{x + 1}} < 0\) có tập nghiệm là

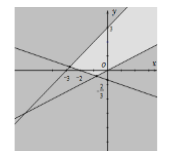
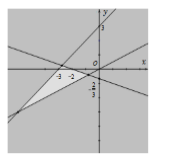
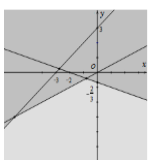
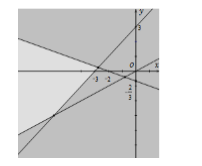
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x - 2y < 0\\x + 3y >  - 2\\y - x < 3\end{array} \right.\) là phần không tô đậm của hình vẽ nào trong các hình vẽ sau?

Tìm tất cả các giá trị thực của tham số $m$ sao cho phương trình sau vô nghiệm \(\left( {2{m^2} + 1} \right){x^2} - 4mx + 2 = 0\)

Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \sqrt {\dfrac{{{x^2} + 5x + 4}}{{2{x^2} + 3x + 1}}} \) là

Số nghiệm của phương trình: $\sqrt {x + 8 - 2\sqrt {x + 7} } = 2 - \sqrt {x + 1 - \sqrt {x + 7} } $ là:

Tập nghiệm của bất phương trình \({x^3} + 3{x^2} - 6x - 8 \ge 0\) là

Tam giác \(ABC\) cân tại \(C\), có \(AB = 9{\rm{cm}}\) và \(AC = \dfrac{{15}}{2}{\rm{cm}}\). Gọi \(D\) là điểm đối xứng của \(B\) qua \(C\). Tính độ dài cạnh \(AD.\) 

Cho ba vector $\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c $ thỏa mãn $\left| {\overrightarrow a } \right| = a,\,\,\left| {\overrightarrow b } \right| = b,\,\,\left| {\overrightarrow c } \right| = c$ và $\overrightarrow a  + \overrightarrow b  + 3\overrightarrow c  = \overrightarrow 0 $. Tính $A = \overrightarrow a .\overrightarrow b  + \overrightarrow b .\overrightarrow c  + \overrightarrow c .\overrightarrow a $

Cho hai đường thẳng \(\left( {{d_1}} \right):mx + y = m + 1\,\,,\left( {{d_2}} \right):x + my = 2\,\) cắt nhau khi và chỉ khi :

Gọi \(H\) là trực tâm của tam giác \(ABC\). Phương trình các cạnh và đường cao của tam giác là \(AB\): \(7x - y + 4 = 0\); \(BH\): \(2x + y - 4 = 0\); \(AH\): \(x - y - 2 = 0\). Phương trình đường cao \(CH\) của tam giác \(ABC\) là

Trong mặt phẳng với hệ tọa độ \(Oxy\) cho \(\Delta ABC\) có \(A\left( {1;\;2} \right)\), \(B\left( {4;\; - 2} \right)\), \(C\left( { - 3;\;5} \right)\). Một véctơ chỉ phương của đường phân giác trong của góc \(A\) là

Trong mặt phẳng với hệ tọa độ $Oxy,$ cho $\Delta ABC$ cân có đáy là $BC.$  Đỉnh $A$  có tọa độ là các số dương, hai điểm $B$  và $C$  nằm trên trục $Ox,$  phương trình cạnh $AB:$ $y = 3\sqrt 7 (x - 1)$. Biết chu vi của $\Delta ABC$ bằng $18,$  tìm tọa độ các đỉnh $A,B,C.$

Cho tam giác $ABC$ có $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ và hai trong ba đường phân giác trong có phương trình lần lượt là $x - 2y - 1 = 0$, $x + 3y - 1 = 0$. Viết phương trình đường thẳng chứa cạnh $BC$.

Có bao nhiêu giá trị $m$ nguyên âm để mọi $x > 0$ đều thoả bất phương trình ${\left( {{x^2} + x + m} \right)^2} \ge {\left( {{x^2} - 3x - m} \right)^2}$?

Phương trình $\left| {x - 2} \right|\left( {x + 1} \right) + m = 0$ có ba nghiệm phân biệt, giá trị thích hợp của tham số $m$ là:

Cho $0 < x,y \le 1;\,\,\,x + y = 4xy.$ Giá trị nhỏ nhất, giá trị lớn nhất của $A = {x^2} + {y^2} - xy$ lần lượt là

Cho hai điểm \(P\left( {6;1} \right)\) và \(Q\left( { - 3; - 2} \right)\) và đường thẳng \(\Delta :2x - y - 1 = 0\). Tọa độ điểm \(M\) thuộc \(\Delta \) sao cho \(MP + MQ\) nhỏ nhất.

Cho ba véc-tơ \(\overrightarrow a \), \(\overrightarrow b \), \(\overrightarrow c \) thỏa mãn: \(\left| {\overrightarrow a } \right| = 4\), \(\left| {\overrightarrow b } \right| = 1\), \(\left| {\overrightarrow c } \right| = 5\) và \(5\left( {\overrightarrow b  - \overrightarrow a } \right) + 3\overrightarrow c  = \overrightarrow 0 \). Khi đó biểu thức \(M = \overrightarrow {a\,} .\overrightarrow {b\,}  + \overrightarrow {b\,} .\overrightarrow {c\,}  + \overrightarrow {c\,} .\overrightarrow {a\,} \) có giá trị là