Câu hỏi:
2 năm trước
Cho tam giác $ABC$ có $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ và hai trong ba đường phân giác trong có phương trình lần lượt là $x - 2y - 1 = 0$, $x + 3y - 1 = 0$. Viết phương trình đường thẳng chứa cạnh $BC$.
Trả lời bởi giáo viên
Đáp án đúng: a
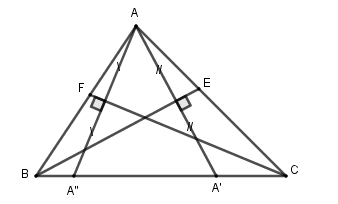
Dễ thấy điểm $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ không thuộc hai đường phân giác $x - 2y - 1 = 0$ và $x + 3y - 1 = 0$. Suy gọi $CF:x - 2y - 1 = 0$, $BE:x + 3y - 1 = 0$ lần lượt là phương trình đường phân giác xuất phát từ đỉnh $C$, $B$(như hình vẽ trên).
Gọi $d$ là đường thẳng qua $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ và vuông góc với $BE$ thì $d$ có VTPT là $\overrightarrow {{n_d}} = \left( {3; - 1} \right)$ nên có phương trình $3\left( {x - \dfrac{4}{5}} \right) - \left( {y - \dfrac{7}{5}} \right) = 0 \Leftrightarrow $$3x - y - 1 = 0$. Tọa độ điểm $M = d \cap BE$ thỏa mãn hệ $\left\{ \begin{array}{l}3x - y - 1 = 0\\x + 3y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{2}{5}\\y = \dfrac{1}{5}\end{array} \right. \Rightarrow $$M\left( {\dfrac{2}{5};\dfrac{1}{5}} \right)$.
Suy ra tọa độ điểm đối xứng với $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ qua $M\left( {\dfrac{2}{5};\dfrac{1}{5}} \right)$ là $A'\left( {0; - 1} \right)$ thì $A' \in BC$$\left( 1 \right)$.
Gọi $d'$ là đường thẳng qua $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ và vuông góc với $CF$ thì $d'$ có VTPT là $\overrightarrow {{n_{d'}}} = \left( {2;1} \right)$ nên có phương trình $2\left( {x - \dfrac{4}{5}} \right) + \left( {y - \dfrac{7}{5}} \right) = 0 \Leftrightarrow $$2x + y - 3 = 0$. Tọa độ điểm $N = d' \cap CF$ thỏa mãn hệ $\left\{ \begin{array}{l}2x + y - 3 = 0\\x - 2y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{7}{5}\\y = \dfrac{1}{5}\end{array} \right. \Rightarrow $$N\left( {\dfrac{7}{5};\dfrac{1}{5}} \right)$.
Suy ra tọa độ điểm đối xứng với $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ qua $N\left( {\dfrac{7}{5};\dfrac{1}{5}} \right)$ là $A''\left( {2; - 1} \right)$ thì $A'' \in BC$$\left( 2 \right)$.
Từ $\left( 1 \right)$ và $\left( 2 \right)$ ta có $\overrightarrow {A'A''} = \left( {2;0} \right)$ là một VTCP của $BC$ suy ra VTPT của $BC$ là $\overrightarrow n = \left( {0;1} \right)$. Do đó phương trình cạnh $BC:0\left( {x - 0} \right) + 1\left( {y + 1} \right) = 0 \Leftrightarrow $ $y + 1 = 0$.
Hướng dẫn giải:
- Tìm tọa độ \(A'\) đối xứng với \(A\) qua phân giác \(BE\).
- Tìm tọa độ \(A''\) đối xứng với \(A\) qua phân giác \(CF\).
- Phương trình \(BC\) cũng là phương trình \(A'A''\).
Giải thích thêm:
Giải thích A' đối xứng với A qua BE thì \(A'\in BC\):
A' đối xứng với A qua BE thì $\widehat {ABE} = \widehat {A'BE}$.
Mà $\widehat {ABE} = \widehat {CBE}$ nên $\widehat {A'BE}=\widehat {CBE}$ hay hai tia BA' và BC trùng nhau.
Do đó \(A'\in BC\).
Câu hỏi khác
- Đề thi kiểm tra giữa học kì 2 - Đề số 3 Toán 10 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 1 Toán 10 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 3 Toán 10 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 2 Toán 10 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 2 - Đề số 2 Toán 10 có lời giải chi tiết
