Để phương trình: $\left| {x + 3} \right|(x - 2) + m - 1 = 0$có đúng một nghiệm, các giá trị của tham số \(m\)là:
Trả lời bởi giáo viên
Ta có $\left| {x + 3} \right|\left( {x - 2} \right) + m - 1 = 0 \Leftrightarrow m = 1 - \left| {x + 3} \right|\left( {x - 2} \right)$
Xét hàm số $y = 1 - \left| {x + 3} \right|(x - 2)$
Ta có $y = \left\{ \begin{array}{l} - {x^2} - x + 7\,\,\;khi\,\,\;x \ge - 3\\{x^2} + x - 5\,\,\;\;\;khi\,\;\;x < - 3\end{array} \right.$
Bảng biến thiên của $y = 1 - \left| {x + 3} \right|(x - 2)$
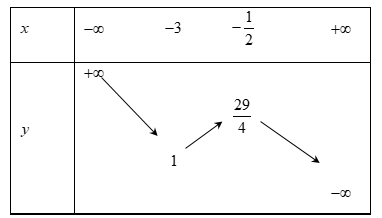
Dựa vào bảng trên phương trình có đúng $1$ nghiệm khi và chỉ khi$\left[ \begin{array}{l}m < 1\\m > \dfrac{{29}}{4}\end{array} \right.$
Hướng dẫn giải:
- Biến đổi phương trình về dạng \(m = f\left( x \right)\).
- Xét hàm \(f\left( x \right)\) kèm theo điều kiện thích hợp của \(x\).
- Phương trình có một nghiệm duy nhất nếu và chỉ nếu đường thẳng \(y = m\) có điểm chung duy nhất với đồ thị hàm số \(y = f\left( x \right)\).

