Câu hỏi:
3 năm trước
Trên đường tròn với điểm gốc là \(A\). Điểm \(M\) thuộc đường tròn sao cho cung lượng giác $AM$ có số đo \({60^0}\). Gọi \(N\) là điểm đối xứng với điểm \(M\) qua trục \(Oy\), số đo cung lượng giác \(AN\) là:
Trả lời bởi giáo viên
Đáp án đúng: d
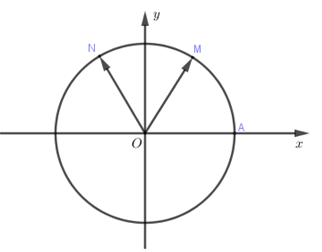
Ta có \(\widehat {AOM} = {60^0}\), \(\widehat {MON} = {60^0}\)
Nên \(\widehat {AON} = {120^0}\).
Khi đó số đo cung lượng giác \(AN\) bằng \({120^0} + k{360^0}\).
Hướng dẫn giải:
- Xác định vị trí các điểm \(M,N\) và xác định góc hình học \(\widehat {AON}\) suy ra số đo cung lượng giác \(AN\)
Giải thích thêm:
Một số em có thể sẽ chọn nhầm đáp án A vì không chú ý \({120^0}\) và \(k2\pi \) không cùng đơn vị đo nên không cộng được.

