Trong mặt phẳng \(\left( {Oxy} \right)\) cho \(\Delta ABC\). Biết phương trình các đường thẳng chứa đường cao \(BH\), phân giác \(AD\) lần lượt là \(3x + 4y + 10 = 0,x - y + 1 = 0\) và điểm \(M\left( {0;2} \right)\) thuộc đường thẳng \(AB\) và \(MC = \sqrt 2 \). Khi đó hoành độ nguyên của điểm \(C\) là
Trả lời bởi giáo viên
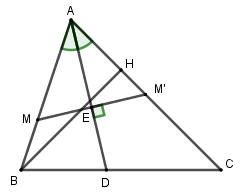
Lấy điểm \(M'\) đối xứng với \(M\) qua \(AD\) thì \(M' \in AC\).
+) Viết phương trình \(MM'\).
\(AD:x - y + 1 = 0\) có \(\overrightarrow {{n_{AD}}} = \left( {1; - 1} \right) \Rightarrow \overrightarrow {{u_{AD}}} = \left( {1;1} \right)\).
Ta có: \(MM' \bot AD\) \( \Rightarrow \overrightarrow {{n_{MM'}}} = \overrightarrow {{u_{AD}}} = \left( {1;1} \right)\)
Đường thẳng \(MM'\) đi qua \(M\left( {0;2} \right)\) và nhận \(\overrightarrow {{n_{MM'}}} = \left( {1;1} \right)\) làm VTPT nên:
\(MM':1\left( {x - 0} \right) + 1\left( {y - 2} \right) = 0\) hay \(x + y - 2 = 0\).
Gọi \(E = MM' \cap AD\), tọa độ \(E\) thỏa mán hệ phương trình \(\left\{ \begin{array}{l}x - y + 1 = 0\\x + y - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{2}\\y = \dfrac{3}{2}\end{array} \right.\) \( \Rightarrow {\rm{E}}\left( {\dfrac{1}{2};\dfrac{3}{2}} \right)\).
Mà \(E\) là trung điểm của \(MM'\) nên \(\left\{ \begin{array}{l}{x_{M'}} = 2{x_E} - {x_M} = 1\\{y_{M'}} = 2{y_E} - {y_M} = - 1\end{array} \right.\) \( \Rightarrow M'\left( {1;1} \right)\).
Ta có: \(BH:3x + 4y + 10 = 0\) \( \Rightarrow \overrightarrow {{n_{BH}}} = \left( {3;4} \right) \Rightarrow \overrightarrow {{u_{BH}}} = \left( {4; - 3} \right)\), \(AC \bot BH \Rightarrow \overrightarrow {{n_{AC}}} = \overrightarrow {{u_{BH}}} = \left( {4; - 3} \right)\).
Đường thẳng \(AC\) đi qua \(M'\left( {1;1} \right)\) và nhận \(\overrightarrow {{n_{AC}}} = \left( {4; - 3} \right)\) làm VTPT nên:
\(AC:4\left( {x - 1} \right) - 3\left( {y - 1} \right) = 0\) hay \(4x - 3y - 1 = 0\).
\(C \in AC\) nên gọi tọa độ của \(C\left( {t;\dfrac{{4t - 1}}{3}} \right)\) với \(t \in \mathbb{Z}\).
\(MC = \sqrt 2 \) \( \Leftrightarrow \sqrt {{{\left( {t - 0} \right)}^2} + {{\left( {\dfrac{{4t - 1}}{3} - 2} \right)}^2}} = \sqrt 2 \) \( \Leftrightarrow {t^2} + {\left( {\dfrac{{4t - 7}}{3}} \right)^2} = 2\) \( \Leftrightarrow 9{t^2} + 16{t^2} - 56t + 49 - 18 = 0\) \( \Leftrightarrow 25{t^2} - 56t + 31 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}t = \dfrac{{31}}{{25}}\left( L \right)\\t = 1\left( {TM} \right)\end{array} \right.\)
Vậy hoành độ nguyên của \(C\) là \(1\).
Hướng dẫn giải:
- Tìm tọa độ điểm đối xứng của \(M\) qua \(AD\).
- Viết phương trình \(AC\).
- Gọi tọa độ của \(C\) theo phương trình vừa viết, lập phương trình dựa vào điều kiện khoảng cách.
- Giải phương trình và kết luận.

