Tính chất hai tiếp tuyến cắt nhau

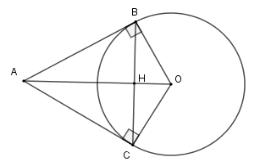
Gọi $H$ là giao của $BC$ với $AO$.

Xét $\left( O \right)$ có hai tiếp tuyến tại $B$ và $C$ cắt nhau tại $A$ nên $AB = AC$ (tính chất)

Lại có $OB = OC$ nên $AO$ là đường trung trực của đoạn $BC$ hay $AO \bot BC$ tại $H$ là trung điểm của $BC$.

Ta chưa kết luận được $H$ có là trung điểm của $AO$ hay không nên đáp án D sai.

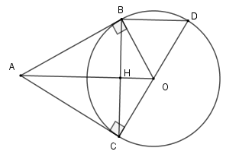
Theo câu trước ta có $AO \bot BC$ (*)

Xét tam giác $BCD$ có $DC$ là đường kính của $\left( O \right)$ và $B \in \left( O \right)$ nên $\Delta BDC$ vuông tại $B$ hay $BD \bot BC$ (**)

Từ (*) và (**) suy ra $BD{\rm{//}}AO$

Mà $AO$ và $AC$ cắt nhau nên $BD$ và $AC$ không thể song song.

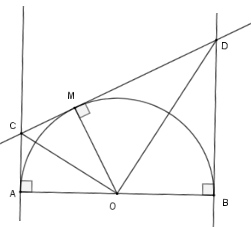
Xét nửa $\left( O \right)$ có $MC$ và $AC$ là hai tiếp tuyến cắt nhau tại $C$ nên $OC$ là phân giác $\widehat {MOA}$ do đó $\widehat {AOC} = \widehat {COM}$

Lại có $MD$ và $BD$ là hai tiếp tuyến cắt nhau tại $D$ nên $OD$ là phân giác $\widehat {MOB}$ do đó $\widehat {DOB} = \widehat {DOM}$

Từ đó $\widehat {AOC} + \widehat {BOD} = \widehat {COM} + \widehat {MOD}$$ = \dfrac{{\widehat {AOC} + \widehat {BOD} + \widehat {COM} + \widehat {MOD}}}{2} = \dfrac{{180^\circ }}{2} = 90^\circ $

Nên $\widehat {COD} = 90^\circ $ hay $\Delta COD$ vuông tại $O$ có $OM$ là đường cao nên $MC.MD = O{M^2}$.

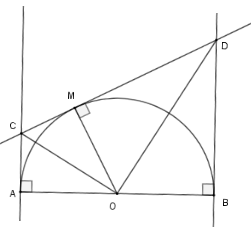
Áp dụng định lý Pytago cho tam giác $BDO$ ta có  $BD = \sqrt {O{D^2} - O{B^2}}  = \sqrt 3 .R$

Mà $MD = BD;MC = AC$ (tính chất hai tiếp tuyến cắt nhau) nên $MD = \sqrt 3 R$

Theo câu trước ta có $MC.MD = O{M^2} $

$\Rightarrow MC = \dfrac{{O{M^2}}}{{MD}} = \dfrac{{{R^2}}}{{\sqrt 3 .R}} = \dfrac{{R\sqrt 3 }}{3}$ nên $AC = \dfrac{{R\sqrt 3 }}{3}$

Vậy $BD = \sqrt 3 R;AC = \dfrac{{\sqrt 3 R}}{3}.$

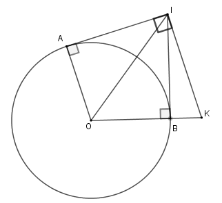
Xét $\left( O \right)$có $IA,IB$ là hai tiếp tuyến cắt nhau tại $I$ nên $\widehat {AOI} = \widehat {KOI}$

Mà $OA{\rm{//}}KI$ (vì cùng vuông góc với $AI$) nên $\widehat {KIO} = \widehat {IOA}$ (hai góc ở vị trí so le trong)

Từ đó $\widehat {KOI} = \widehat {KIO}$ suy ra $\Delta KOI$ cân tại $K \Rightarrow KI = KO$.

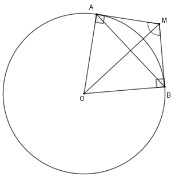
Xét $\left( O \right)$ có $MA = MB$; $\widehat {AMO} = \widehat {BMO}$ (tính chất hai tiếp tuyến cắt nhau)

Nên $\widehat {AMO} = 60^\circ $. Xét tam giác vuông $AOM$ có $AM = AO.cot\widehat {AMO} = \dfrac{{R\sqrt 3 }}{3}$ nên $MA = MB = \dfrac{{R\sqrt 3 }}{3}$

Lại có $\widehat {AOB} + \widehat {AMB} = 180^\circ  \Rightarrow \widehat {AOB} = 60^\circ $ suy ra $\Delta AOB$ là tam giác đều $ \Rightarrow AB = OB = OA = R$

Chu vi tam giác $MAB$ là $MA + MB + AB = \dfrac{{R\sqrt 3 }}{3} + \dfrac{{R\sqrt 3 }}{3} + R = 6\left( {3 + 2\sqrt 3 } \right)$

$ \Leftrightarrow R\left( {\dfrac{{3 + 2\sqrt 3 }}{3}} \right) = 6\left( {3 + 2\sqrt 3 } \right) \Rightarrow R = 18\,cm$ nên $AB = 18\,cm$.

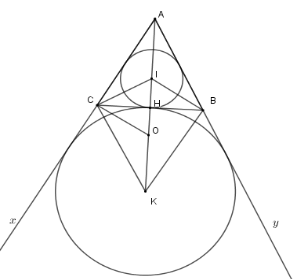
Vì tam giác $ABC$ cân tại $A$ nên $I;K \in $ đường thẳng $AH$ với $\left\{ H \right\} = BC \cap AI$

Ta có $\widehat {HCI} = \dfrac{1}{2}\widehat {HCA};\widehat {KCH} = \dfrac{1}{2}\widehat {xCH}$$ \Rightarrow \widehat {ICK} = \widehat {ICH} + \widehat {HCK} = \dfrac{1}{2}\left( {\widehat {ACH} + \widehat {HCx}} \right) = 90^\circ $

Tương tự ta cũng có $\widehat {IBK} = 90^\circ $

Xét hai tam giác vuông $ICK$ và $IBK$ có $OI = OK = OB = OC = \dfrac{{IK}}{2}$

Nên bốn điểm $B;I;C;K$ nằm trên đường tròn $\left( {O;\dfrac{{IK}}{2}} \right)$.

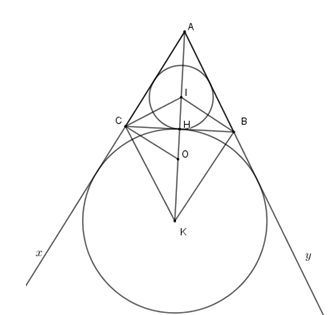
Ta có tam giác $CKI$ vuông nên \(\widehat {CKI} + \widehat {CIO} = 90^\circ \), lại có \(\widehat {CIK} + \widehat {ICH} = 90^\circ \) mà $CI$ là phân giác \(\widehat {ACB}\) nên $\widehat {ACI} =\widehat {CKO} $.

Có tam giác $COK$ cân tại $O$ nên \(\widehat {ACI} = \widehat {OCK}\)\( (=\widehat {CKO})\)

Nên $\widehat {ICO}+\widehat {ACI}=\widehat {ICO}+\widehat {OCK}  = 90 ^\circ $

Suy ra \(\widehat {ACO} = 90^\circ \) $ \Rightarrow OC \bot AC.$

Ta có $HB = HC$ ($AK$ là trung trực của$BC$ ) \( \Rightarrow HB = \dfrac{{BC}}{2} = 12\).

Theo Pytago ta có \(AH = \sqrt {A{C^2} - H{C^2}}  = 16\)

Lại có  \(\Delta ACH\backsim\Delta COH\) (hai tam giác vuông có $\widehat {COH} = \widehat {ACH}$ vì cùng phụ với $\widehat {HCO}$)

\( \Rightarrow \dfrac{{AH}}{{AC}} = \dfrac{{HC}}{{CO}}\)  \( \Rightarrow CO = \dfrac{{AC.HC}}{{AH}} = 15\) .

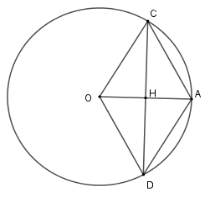
Gọi $H$ là giao của $OA$ và $CD$

Xét $\left( O \right)$ có $OA \bot CD$ tại $H$ nên $H$ là trung điểm của $CD$

Xét tứ giác $OCAD$ có hai đường chéo $OA$ và $CD$ vuông góc với nhau và giao nhau tại trung điểm $H$ mỗi đường nên $OCAD$ là hình thoi. 

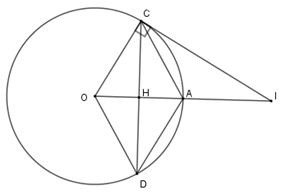
Xét tam giác $COA$ có  $OC = OA = R$ và $OC = AC$ (do $OCAD$ là hình thoi) nên $\Delta COA$ là tam giác đều

$ \Rightarrow \widehat {COI} = 60^\circ .$

Xét tam giác vuông $OCI$ có $CI = OC.\tan 60^\circ  = R\sqrt 3 $.

Vậy $CI = R\sqrt 3 $.

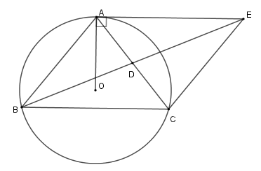
Vì tam giác $ABC$ cân tại $A$ có $O$ là tâm đường tròn ngoại tiếp nên đường thẳng $AO \bot BC$

Lại có $AO \bot AE$ (tính chất tiếp tuyến ) nên $AE{\rm{//}}BC$

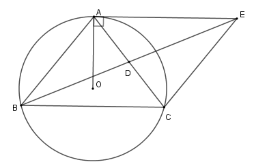
Vì $AE{\rm{//}}BC$ nên $\widehat {EAC} = \widehat {ACB}$ (hai góc ở vị trí so le trong) , lại có $\widehat {ADE} = \widehat {BDC}$ (đối đỉnh) và $AD = DC$

Nên $\Delta ADE = \Delta CDB\left( {g - c - g} \right) $

$\Rightarrow AE = BC$

Tứ giác $AECB$ có $AE = BC;AE{\rm{//}}BC$ nên $AECB$ là hình bình hành.

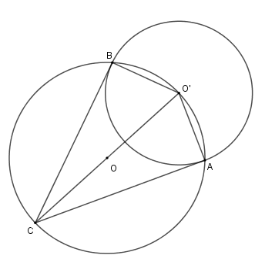
Xét đường tròn $\left( O \right)$ có $O'C$ là đường kính, suy ra $\widehat {CBO'} = \widehat {CAO'} = 90^\circ $ hay $CB \bot O'B$ tại $B$ và $AC \bot AO'$ tại $A$.

Do đó $AB,BC$ là hai tiếp tuyến của $\left( {O'} \right)$ nên $AC = CB$ (tính chất hai tiếp tuyến cắt nhau)

Nên A, B, C đúng.

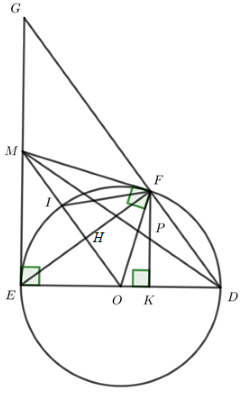
* Vì ME  là tiếp tuyến của \(\left( O \right)\) nên  ME  vuông góc với OE, suy ra tam giác MOE nội tiếp đường tròn đường kính MO  (1)

Vì  MF  là tiếp tuyến của \(\left( O \right)\) nên  MF  vuông góc với OF, suy ra tam giác MOF nội tiếp đường tròn đường kính MO  (2)

Từ (1) và (2) suy ra M, E, O, F cùng thuộc một đường tròn nên A đúng.

* Gọi \(MO \cap EF = \left\{ H \right\}\)

Vì M là giao điểm của 2 tiếp tuyến ME và MF của \(\left( O \right)\)

\( \Rightarrow ME = MF\) (tính chất) mà \(OE = OF = R\) (gt)

\( \Rightarrow \) MO là đường trung trực của EF

\( \Rightarrow MO \bot EF\)

\( \Rightarrow \angle IFE + \angle OIF = {90^o}\,\)

Vì \(OI = OF = R\)  nên tam giác OIF cân tại O

\( \Rightarrow \angle OIF = \angle OFI\)  mà  \(\angle MFI + \angle OFI = {90^o}\,;\,\,\,\angle IFE + \angle OIF = {90^o}\)

\( \Rightarrow \angle MFI = \angle IFE\)

\( \Rightarrow \) FI là phân giác của \(\angle MFE\)   (1)

Vì M là giao điểm của 2 tiếp tuyến ME và MF của \(\left( O \right)\)

\( \Rightarrow \) MI là phân giác của \(\angle EMF\) (tính chất)   (2)

Từ (1) và (2) \( \Rightarrow \) I là tâm đường tròn nội tiếp tam giác MEF

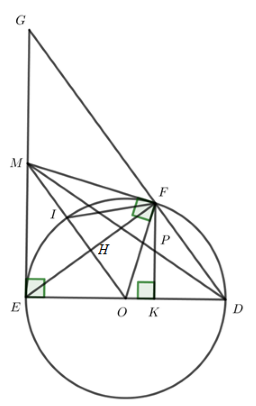
Gọi G là giao điểm của tia DF và tia EM.

Ta có \(\angle EFD = {90^o}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow EF \bot DG\) mà \(EF \bot OM\) (cmt)

\( \Rightarrow OM//DG\) (từ vuông góc đến song song)

Tam giác EDG có \(OE = OD\,\,;\,\,OM//DG\,\, \Rightarrow ME = MG\)(tính chất đường trung bình)

Áp dụng định lý Ta-let cho tam giác EDM có \(PK//ME\) (cùng vuông góc với ED) ta được:   \(\dfrac{{PK}}{{ME}} = \dfrac{{DP}}{{DM}}\)     (3)

Áp dụng định lý Ta-let cho tam giác MDG có \(PF//MG\) (cùng vuông góc với ED) ta được:   \(\dfrac{{PF}}{{MG}} = \dfrac{{DP}}{{DM}}\)     (4)

Từ (3) và (4) suy ra   \(\dfrac{{PK}}{{ME}} = \dfrac{{PF}}{{MG}}\)  mà  \(ME = MG\) (cmt)

\( \Rightarrow PK = PF\,\, \Rightarrow \)  P là trung điểm của FK. Suy ra \(FP = PK = \dfrac{4}{2} = 2cm\)

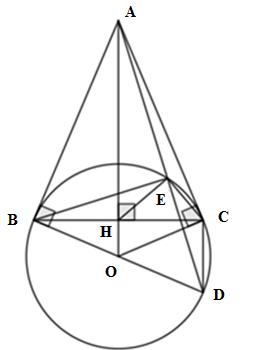
* Ta có AB, AC là hai tiếp tuyến của \(\left( O \right)\)\( \Rightarrow \angle OBA = \angle OCA = {90^o}\)

\( \Rightarrow \) B, C cùng thuộc đường tròn đường kính OA

 \( \Rightarrow \) A, B, O, C cùng thuộc một đường tròn đường kính OA. Do đó A sai.

* Ta có AB, AC là hai tiếp tuyến của \(\left( O \right)\) cắt nhau tại A

\( \Rightarrow \) \(AB = AC\) và AO là phân giác \(\angle BAC\)  (tính chất 2 tiếp tuyến cắt nhau)

\( \Rightarrow \Delta ABC\) là tam giác cân tại A

\( \Rightarrow \) AO vừa là phân giác \(\angle BAC\)  vừa là đường trung trực của BC (tính chất tam giác cân) nên B sai.

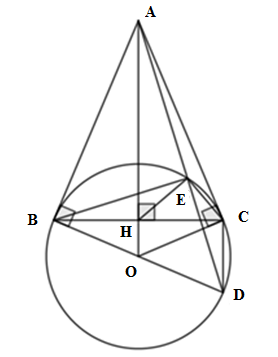
Ta có D đối xứng với B qua O \( \Rightarrow \) BD là đường kính của \(\left( O \right)\) mà \(E \in \left( O \right)\)

\( \Rightarrow \) \(\angle BED = {90^o}\)

Xét \(\Delta BED\) và \(\Delta ABD\) có: \(\angle BED = \angle ABD = {90^o}\), \(\angle D\) chung

\( \Rightarrow \Delta BED \backsim \Delta ABD\left( {g - g} \right) \Rightarrow \dfrac{{DE}}{{BE}} = \dfrac{{BD}}{{BA}}.\)

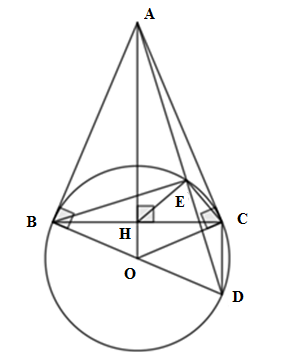
\(\angle BCD = {90^o}\) (góc nội tiếp chắn nửa đường tròn)

\(\angle AHB = {90^o}\) (AO là trung trực của BC)

Xét \(\Delta BCD\) và \(\Delta AHB\) có: \(\angle BCD = \angle AHB = {90^o},\;\angle BDC = \angle ABH\) (BA là tiếp tuyến của \(\left( O \right)\) tại B)

\( \Rightarrow \Delta BCD \backsim \Delta AHB\;\left( {g - g} \right) \)\(\Rightarrow \dfrac{{BD}}{{BA}} = \dfrac{{CD}}{{BH}}\)  mà theo câu trước \(\dfrac{{DE}}{{BE}} = \dfrac{{BD}}{{BA}}\) \( \Rightarrow \dfrac{{DE}}{{BE}} = \dfrac{{CD}}{{BH}}\)

Xét \(\Delta BHE\) và \(\Delta DCE\) có  \(\dfrac{{DE}}{{BE}} = \dfrac{{CD}}{{BH}}\)\( \Rightarrow \Delta BHE \backsim \Delta DCE \Rightarrow \angle BEH = \angle DEC\)   (2 góc tương ứng)

\( \Rightarrow \angle BEH + \angle HED = \angle DEC + \angle HED \)\(\Rightarrow \angle BED = \angle HEC\)

Mà \(\angle BED = {90^o}\) (chứng minh trên)

Vậy \(\angle HEC = {90^o}\)

Vì hai tiếp tuyến của đường tròn \(\left( O \right)\) cắt nhau tại \(A\) nên \(\widehat {ACO} = \widehat {ABO} = {90^0} \Rightarrow \widehat {CAB} + \widehat {COB} = {360^0} - {180^0} = {180^0}\)

Mà \(\widehat {CAB} = {50^0}\) nên \(\widehat {COB} = {180^0} - {50^0} = {130^0}\)

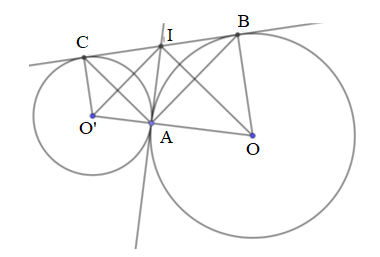
Ta có \(IO\) là tia phân giác của \(\widehat {BIA}\)

\(IO'\) là tia phân giác của \(\widehat {CIA}\)

Mà \(\widehat {BIA} + \widehat {CIA} = {180^0} \Rightarrow \widehat {OIO'} = {90^0}\)

Tam giác \(OIO'\) vuông tại \(I\) có \(IA\) là đường cao nên \(I{A^2} = AO.AO' = 9.4 = 36 \Rightarrow IA = 6cm\).

\( \Rightarrow IA = IB = IC = 6cm\) (tính chất hai tiếp tuyến cắt nhau)

Vậy \(BC = 2IA = 2.6 = 12\left( {cm} \right)\).