Câu hỏi:
3 năm trước
Cho đường tròn $\left( O \right)$, bán kính $OA$. Dây $CD$ là đường trung trực của $OA$.
Kẻ tiếp tuyến với đường tròn tại $C$, tiếp tuyến này cắt đường thẳng $OA$ tại $I$. Biết $OA = R$. Tính $CI$ theo $R$.
Trả lời bởi giáo viên
Đáp án đúng: d
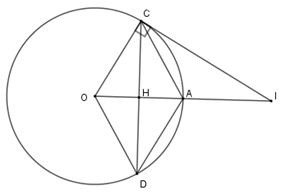
Xét tam giác $COA$ có $OC = OA = R$ và $OC = AC$ (do $OCAD$ là hình thoi) nên $\Delta COA$ là tam giác đều
$ \Rightarrow \widehat {COI} = 60^\circ .$
Xét tam giác vuông $OCI$ có $CI = OC.\tan 60^\circ = R\sqrt 3 $.
Vậy $CI = R\sqrt 3 $.
Hướng dẫn giải:
Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông

