Trả lời bởi giáo viên
Đáp án đúng: d
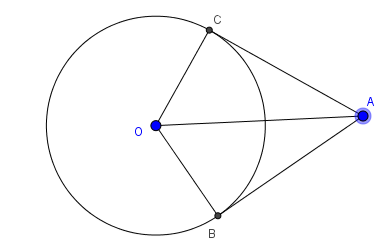
Xét \(\left( O \right)\) có \(AB,AC\) là hai tiếp tuyến cắt nhau tại \(A\) nên \(AB = AC;\,\widehat {CAO} = \widehat {BAO};\widehat {BOA} = \widehat {COA}\)
Xét \(\Delta ABO\) vuông tại \(B\) có \(OB = 3cm;\,OA = 5cm\), theo định lý Pytago ta có \(AB = \sqrt {O{A^2} - O{B^2}} = \sqrt {{5^2} - {3^2}} = 4\,cm\)
Nên \(AC = AB = 4cm\) hay đáp án A đúng.
Xét tam giác \(ABO\) vuông tại \(B\) có \(\sin \widehat {ABO} = \dfrac{{AB}}{{OA}} = \dfrac{4}{5}\) nên C đúng. Mà \(\widehat {BOA} = \widehat {COA}\) nên \(\sin \widehat {COA} = \dfrac{4}{5}\) do đó D sai.
Hướng dẫn giải:
Sử dụng kiến thức về hai tiếp tuyến cắt nhau
Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:
- Điểm đó cách đều hai tiếp điểm.
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của các góc tạo bởi hai tiếp tuyến.
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.
Sử dụng định lý Pytago và tỉ số lượng giác của góc nhọn
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
