Trả lời bởi giáo viên
Đáp án đúng: d
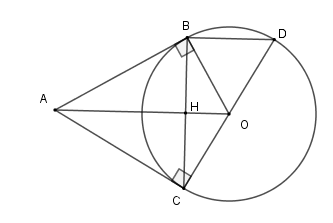
Gọi \(H\) là giao của \(BC\) với \(AO\).
Xét \(\left( O \right)\) có hai tiếp tuyến tại \(B\) và \(C\) cắt nhau tại \(A\) nên \(AB = AC\) (tính chất)
Lại có \(OB = OC\) nên \(AO\) là đường trung trực của đoạn \(BC\) hay \(AO \bot BC\) tại \(H\) là trung điểm của \(BC\).
Xét tam giác \(BCD\) có \(H\) là trung điểm \(BC\) và \(O\) là trung điểm \(DC\) nên là đường trung bình của tam giác \(BCD\)
Suy ra \(BD = 2.OH\)
Xét tam giác \(ABO\) vuông tại \(B\) có \(BH\) là đường cao. Theo hệ thức lượng trong tam giác vuông ta có \(B{O^2} = OH.OA \Leftrightarrow OH = \dfrac{{O{B^2}}}{{OA}} = \dfrac{9}{5} = 1,8\,cm\)
Từ đó \(BD = 2.OH = 2.1,8 = 3,6\,cm\)
Hướng dẫn giải:
Sử dụng quan hệ từ vuông góc đến song song
Sử dụng hệ thức lượng trong tam giác vuông
Sử dụng tính chất đường trung bình của tam giác
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
