Câu hỏi:
2 năm trước
Cho tam giác $ABC$ cân tại $A$, $I$ là tâm đường tròn nội tiếp, $K$ là tâm đường tròn bàng tiếp trong góc $A.$ Gọi $O$ là trung điểm của $IK.$
Tính bán kính đường tròn $(O)$ biết $AB = AC = 20cm,BC = 24cm.$
Trả lời bởi giáo viên
Đáp án đúng: b
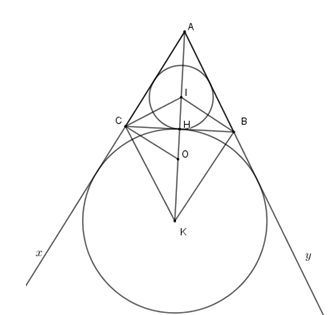
Ta có tam giác $CKI$ vuông nên \(\widehat {CKI} + \widehat {CIO} = 90^\circ \), lại có \(\widehat {CIK} + \widehat {ICH} = 90^\circ \) mà $CI$ là phân giác \(\widehat {ACB}\) nên $\widehat {ACI} =\widehat {CKO} $.
Có tam giác $COK$ cân tại $O$ nên \(\widehat {ACI} = \widehat {OCK}\)\( (=\widehat {CKO})\)
Nên $\widehat {ICO}+\widehat {ACI}=\widehat {ICO}+\widehat {OCK} = 90 ^\circ $
Suy ra \(\widehat {ACO} = 90^\circ \) $ \Rightarrow OC \bot AC.$
Ta có $HB = HC$ ($AK$ là trung trực của$BC$ ) \( \Rightarrow HB = \dfrac{{BC}}{2} = 12\).
Theo Pytago ta có \(AH = \sqrt {A{C^2} - H{C^2}} = 16\)
Lại có \(\Delta ACH\backsim\Delta COH\) (hai tam giác vuông có $\widehat {COH} = \widehat {ACH}$ vì cùng phụ với $\widehat {HCO}$)
\( \Rightarrow \dfrac{{AH}}{{AC}} = \dfrac{{HC}}{{CO}}\) \( \Rightarrow CO = \dfrac{{AC.HC}}{{AH}} = 15\) .
Hướng dẫn giải:
Sử dụng tính chất hai tiếp tuyến cắt nhau và công thức chu vi tam giác
Câu hỏi khác
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
