Câu hỏi:
2 năm trước
Cho tam giác $ABC$ cân tại $A$, $I$ là tâm đường tròn nội tiếp, $K$ là tâm đường tròn bàng tiếp trong góc $A.$ Gọi $O$ là trung điểm của $IK.$
Tâm của đường tròn đi qua bốn điểm $B,I,C,K$ là
Trả lời bởi giáo viên
Đáp án đúng: a
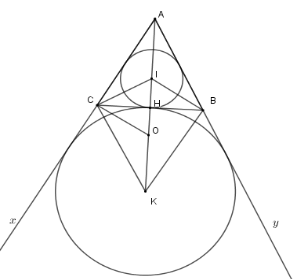
Vì tam giác $ABC$ cân tại $A$ nên $I;K \in $ đường thẳng $AH$ với $\left\{ H \right\} = BC \cap AI$
Ta có $\widehat {HCI} = \dfrac{1}{2}\widehat {HCA};\widehat {KCH} = \dfrac{1}{2}\widehat {xCH}$$ \Rightarrow \widehat {ICK} = \widehat {ICH} + \widehat {HCK} = \dfrac{1}{2}\left( {\widehat {ACH} + \widehat {HCx}} \right) = 90^\circ $
Tương tự ta cũng có $\widehat {IBK} = 90^\circ $
Xét hai tam giác vuông $ICK$ và $IBK$ có $OI = OK = OB = OC = \dfrac{{IK}}{2}$
Nên bốn điểm $B;I;C;K$ nằm trên đường tròn $\left( {O;\dfrac{{IK}}{2}} \right)$.
Hướng dẫn giải:
Xác định điểm cách đều bốn điểm, điểm đó chính là tâm của đường tròn.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
