Câu hỏi:
2 năm trước
Cho đường tròn \(\left( {O;R} \right)\) và điểm A nằm ngoài \(\left( O \right)\). Từ A kẻ hai tiếp tuyến AB, AC với \(\left( O \right)\) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với \(\left( O \right)\) (E không trùng với D).
Chọn câu đúng nhất.
Trả lời bởi giáo viên
Đáp án đúng: d
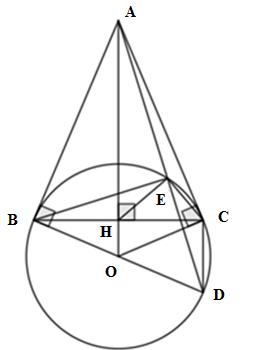
* Ta có AB, AC là hai tiếp tuyến của \(\left( O \right)\)\( \Rightarrow \angle OBA = \angle OCA = {90^o}\)
\( \Rightarrow \) B, C cùng thuộc đường tròn đường kính OA
\( \Rightarrow \) A, B, O, C cùng thuộc một đường tròn đường kính OA. Do đó A sai.
* Ta có AB, AC là hai tiếp tuyến của \(\left( O \right)\) cắt nhau tại A
\( \Rightarrow \) \(AB = AC\) và AO là phân giác \(\angle BAC\) (tính chất 2 tiếp tuyến cắt nhau)
\( \Rightarrow \Delta ABC\) là tam giác cân tại A
\( \Rightarrow \) AO vừa là phân giác \(\angle BAC\) vừa là đường trung trực của BC (tính chất tam giác cân) nên B sai.
Hướng dẫn giải:
+ Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền
+ Áp dụng tính chất hai tiếp tuyến cắt nhau và tính chất của tam giác cân để chứng minh
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
