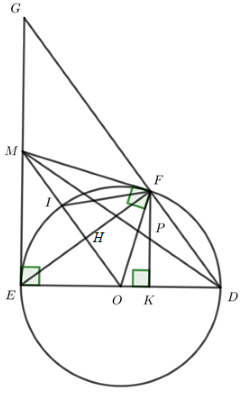
Cho đường tròn \(\left( {O;R} \right)\). Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF đến đường tròn (với E, F là các tiếp điểm). Đoạn OM cắt đường tròn \(\left( {O;R} \right)\) tại I. Kẻ đường kính ED của \(\left( {O;R} \right)\). Hạ FK vuông góc với ED. Gọi P là giao điểm của MD và FK.
Chọn câu đúng.
Trả lời bởi giáo viên
* Vì ME là tiếp tuyến của \(\left( O \right)\) nên ME vuông góc với OE, suy ra tam giác MOE nội tiếp đường tròn đường kính MO (1)
Vì MF là tiếp tuyến của \(\left( O \right)\) nên MF vuông góc với OF, suy ra tam giác MOF nội tiếp đường tròn đường kính MO (2)
Từ (1) và (2) suy ra M, E, O, F cùng thuộc một đường tròn nên A đúng.
* Gọi \(MO \cap EF = \left\{ H \right\}\)
Vì M là giao điểm của 2 tiếp tuyến ME và MF của \(\left( O \right)\)
\( \Rightarrow ME = MF\) (tính chất) mà \(OE = OF = R\) (gt)
\( \Rightarrow \) MO là đường trung trực của EF
\( \Rightarrow MO \bot EF\)
\( \Rightarrow \angle IFE + \angle OIF = {90^o}\,\)
Vì \(OI = OF = R\) nên tam giác OIF cân tại O
\( \Rightarrow \angle OIF = \angle OFI\) mà \(\angle MFI + \angle OFI = {90^o}\,;\,\,\,\angle IFE + \angle OIF = {90^o}\)
\( \Rightarrow \angle MFI = \angle IFE\)
\( \Rightarrow \) FI là phân giác của \(\angle MFE\) (1)
Vì M là giao điểm của 2 tiếp tuyến ME và MF của \(\left( O \right)\)
\( \Rightarrow \) MI là phân giác của \(\angle EMF\) (tính chất) (2)
Từ (1) và (2) \( \Rightarrow \) I là tâm đường tròn nội tiếp tam giác MEF
Hướng dẫn giải:
+ Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền
+ Tâm đường tròn nội tiếp tam giác là giao ba đường phân giác
+ Tâm đường tròn ngoại tiếp tam giác là giao ba đường trung trực

