Cho đường tròn \(\left( {O;R} \right)\) và điểm A nằm ngoài \(\left( O \right)\). Từ A kẻ hai tiếp tuyến AB, AC với \(\left( O \right)\) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với \(\left( O \right)\) (E không trùng với D).

Số đo góc \(HEC\) là

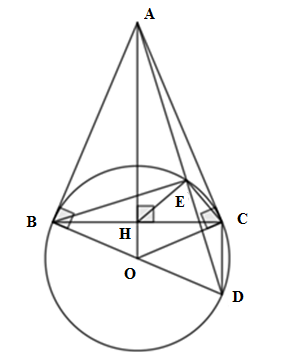
\(\angle BCD = {90^o}\) (góc nội tiếp chắn nửa đường tròn)

\(\angle AHB = {90^o}\) (AO là trung trực của BC)

Xét \(\Delta BCD\) và \(\Delta AHB\) có: \(\angle BCD = \angle AHB = {90^o},\;\angle BDC = \angle ABH\) (BA là tiếp tuyến của \(\left( O \right)\) tại B)

\( \Rightarrow \Delta BCD \backsim \Delta AHB\;\left( {g - g} \right) \)\(\Rightarrow \dfrac{{BD}}{{BA}} = \dfrac{{CD}}{{BH}}\)  mà theo câu trước \(\dfrac{{DE}}{{BE}} = \dfrac{{BD}}{{BA}}\) \( \Rightarrow \dfrac{{DE}}{{BE}} = \dfrac{{CD}}{{BH}}\)

Xét \(\Delta BHE\) và \(\Delta DCE\) có  \(\dfrac{{DE}}{{BE}} = \dfrac{{CD}}{{BH}}\)\( \Rightarrow \Delta BHE \backsim \Delta DCE \Rightarrow \angle BEH = \angle DEC\)   (2 góc tương ứng)

\( \Rightarrow \angle BEH + \angle HED = \angle DEC + \angle HED \)\(\Rightarrow \angle BED = \angle HEC\)

Mà \(\angle BED = {90^o}\) (chứng minh trên)

Vậy \(\angle HEC = {90^o}\)