Câu hỏi:
2 năm trước
Cho nửa đường tròn tâm $O$, đường kính $AB$. Vẽ các tiếp tuyến $Ax,By$ với nữa đường tròn cùng phía đối với $AB$. Từ điểm $M$ trên nửa đường tròn ($M$ khác $A,B$ ) vẽ tiếp tuyến với nửa đường tròn, cắt $Ax$ và $By$ lần lượt tại $C$ và $D$ .
Cho $OD = BA = 2R$ . Tính $AC$ và $BD$ theo $R.$
Trả lời bởi giáo viên
Đáp án đúng: d
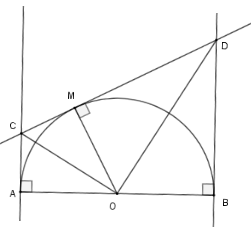
Áp dụng định lý Pytago cho tam giác $BDO$ ta có $BD = \sqrt {O{D^2} - O{B^2}} = \sqrt 3 .R$
Mà $MD = BD;MC = AC$ (tính chất hai tiếp tuyến cắt nhau) nên $MD = \sqrt 3 R$
Theo câu trước ta có $MC.MD = O{M^2} $
$\Rightarrow MC = \dfrac{{O{M^2}}}{{MD}} = \dfrac{{{R^2}}}{{\sqrt 3 .R}} = \dfrac{{R\sqrt 3 }}{3}$ nên $AC = \dfrac{{R\sqrt 3 }}{3}$
Vậy $BD = \sqrt 3 R;AC = \dfrac{{\sqrt 3 R}}{3}.$
Hướng dẫn giải:
Sử dụng định lý Pytago và hệ thức lượng trong tam giác vuông.
Câu hỏi khác
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
