Tứ giác $OCAD$ là hình gì?
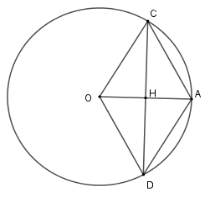
Gọi $H$ là giao của $OA$ và $CD$
Xét $\left( O \right)$ có $OA \bot CD$ tại $H$ nên $H$ là trung điểm của $CD$
Xét tứ giác $OCAD$ có hai đường chéo $OA$ và $CD$ vuông góc với nhau và giao nhau tại trung điểm $H$ mỗi đường nên $OCAD$ là hình thoi.
Chọn khẳng định đúng.
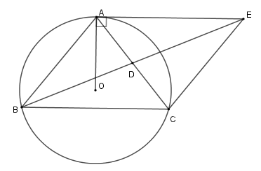
Vì tam giác $ABC$ cân tại $A$ có $O$ là tâm đường tròn ngoại tiếp nên đường thẳng $AO \bot BC$
Lại có $AO \bot AE$ (tính chất tiếp tuyến ) nên $AE{\rm{//}}BC$
Vẽ đường kính $CD$ của $\left( O \right).$ Khi đó
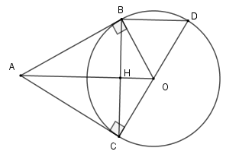
Theo câu trước ta có $AO \bot BC$ (*)
Xét tam giác $BCD$ có $DC$ là đường kính của $\left( O \right)$ và $B \in \left( O \right)$ nên $\Delta BDC$ vuông tại $B$ hay $BD \bot BC$ (**)
Từ (*) và (**) suy ra $BD{\rm{//}}AO$
Mà $AO$ và $AC$ cắt nhau nên $BD$ và $AC$ không thể song song.
Chọn khẳng định sai ?
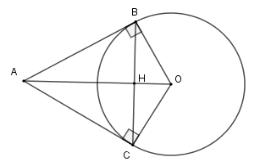
Gọi $H$ là giao của $BC$ với $AO$.
Xét $\left( O \right)$ có hai tiếp tuyến tại $B$ và $C$ cắt nhau tại $A$ nên $AB = AC$ (tính chất)
Lại có $OB = OC$ nên $AO$ là đường trung trực của đoạn $BC$ hay $AO \bot BC$ tại $H$ là trung điểm của $BC$.
Ta chưa kết luận được $H$ có là trung điểm của $AO$ hay không nên đáp án D sai.
Chọn khẳng định sai ?

Gọi $H$ là giao của $BC$ với $AO$.
Xét $\left( O \right)$ có hai tiếp tuyến tại $B$ và $C$ cắt nhau tại $A$ nên $AB = AC$ (tính chất)
Lại có $OB = OC$ nên $AO$ là đường trung trực của đoạn $BC$ hay $AO \bot BC$ tại $H$ là trung điểm của $BC$.
Ta chưa kết luận được $H$ có là trung điểm của $AO$ hay không nên đáp án D sai.
Cho $OD = BA = 2R$ . Tính $AC$ và $BD$ theo $R.$
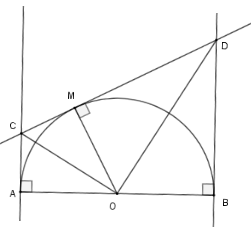
Áp dụng định lý Pytago cho tam giác $BDO$ ta có $BD = \sqrt {O{D^2} - O{B^2}} = \sqrt 3 .R$
Mà $MD = BD;MC = AC$ (tính chất hai tiếp tuyến cắt nhau) nên $MD = \sqrt 3 R$
Theo câu trước ta có $MC.MD = O{M^2} $
$\Rightarrow MC = \dfrac{{O{M^2}}}{{MD}} = \dfrac{{{R^2}}}{{\sqrt 3 .R}} = \dfrac{{R\sqrt 3 }}{3}$ nên $AC = \dfrac{{R\sqrt 3 }}{3}$
Vậy $BD = \sqrt 3 R;AC = \dfrac{{\sqrt 3 R}}{3}.$
Khi đó $MC.MD$ bằng
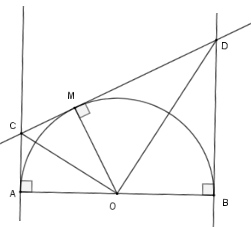
Xét nửa $\left( O \right)$ có $MC$ và $AC$ là hai tiếp tuyến cắt nhau tại $C$ nên $OC$ là phân giác $\widehat {MOA}$ do đó $\widehat {AOC} = \widehat {COM}$
Lại có $MD$ và $BD$ là hai tiếp tuyến cắt nhau tại $D$ nên $OD$ là phân giác $\widehat {MOB}$ do đó $\widehat {DOB} = \widehat {DOM}$
Từ đó $\widehat {AOC} + \widehat {BOD} = \widehat {COM} + \widehat {MOD}$$ = \dfrac{{\widehat {AOC} + \widehat {BOD} + \widehat {COM} + \widehat {MOD}}}{2} = \dfrac{{180^\circ }}{2} = 90^\circ $
Nên $\widehat {COD} = 90^\circ $ hay $\Delta COD$ vuông tại $O$ có $OM$ là đường cao nên $MC.MD = O{M^2}$.
Khi đó $MC.MD$ bằng

Xét nửa $\left( O \right)$ có $MC$ và $AC$ là hai tiếp tuyến cắt nhau tại $C$ nên $OC$ là phân giác $\widehat {MOA}$ do đó $\widehat {AOC} = \widehat {COM}$
Lại có $MD$ và $BD$ là hai tiếp tuyến cắt nhau tại $D$ nên $OD$ là phân giác $\widehat {MOB}$ do đó $\widehat {DOB} = \widehat {DOM}$
Từ đó $\widehat {AOC} + \widehat {BOD} = \widehat {COM} + \widehat {MOD}$$ = \dfrac{{\widehat {AOC} + \widehat {BOD} + \widehat {COM} + \widehat {MOD}}}{2} = \dfrac{{180^\circ }}{2} = 90^\circ $
Nên $\widehat {COD} = 90^\circ $ hay $\Delta COD$ vuông tại $O$ có $OM$ là đường cao nên $MC.MD = O{M^2}$.
Tính bán kính đường tròn $(O)$ biết $AB = AC = 20cm,BC = 24cm.$
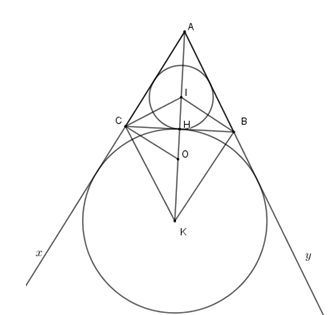
Ta có tam giác $CKI$ vuông nên \(\widehat {CKI} + \widehat {CIO} = 90^\circ \), lại có \(\widehat {CIK} + \widehat {ICH} = 90^\circ \) mà $CI$ là phân giác \(\widehat {ACB}\) nên $\widehat {ACI} =\widehat {CKO} $.
Có tam giác $COK$ cân tại $O$ nên \(\widehat {ACI} = \widehat {OCK}\)\( (=\widehat {CKO})\)
Nên $\widehat {ICO}+\widehat {ACI}=\widehat {ICO}+\widehat {OCK} = 90 ^\circ $
Suy ra \(\widehat {ACO} = 90^\circ \) $ \Rightarrow OC \bot AC.$
Ta có $HB = HC$ ($AK$ là trung trực của$BC$ ) \( \Rightarrow HB = \dfrac{{BC}}{2} = 12\).
Theo Pytago ta có \(AH = \sqrt {A{C^2} - H{C^2}} = 16\)
Lại có \(\Delta ACH\backsim\Delta COH\) (hai tam giác vuông có $\widehat {COH} = \widehat {ACH}$ vì cùng phụ với $\widehat {HCO}$)
\( \Rightarrow \dfrac{{AH}}{{AC}} = \dfrac{{HC}}{{CO}}\) \( \Rightarrow CO = \dfrac{{AC.HC}}{{AH}} = 15\) .
Tâm của đường tròn đi qua bốn điểm $B,I,C,K$ là
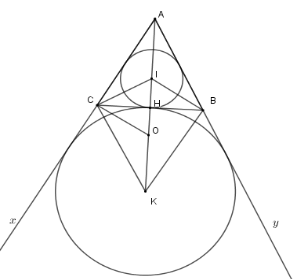
Vì tam giác $ABC$ cân tại $A$ nên $I;K \in $ đường thẳng $AH$ với $\left\{ H \right\} = BC \cap AI$
Ta có $\widehat {HCI} = \dfrac{1}{2}\widehat {HCA};\widehat {KCH} = \dfrac{1}{2}\widehat {xCH}$$ \Rightarrow \widehat {ICK} = \widehat {ICH} + \widehat {HCK} = \dfrac{1}{2}\left( {\widehat {ACH} + \widehat {HCx}} \right) = 90^\circ $
Tương tự ta cũng có $\widehat {IBK} = 90^\circ $
Xét hai tam giác vuông $ICK$ và $IBK$ có $OI = OK = OB = OC = \dfrac{{IK}}{2}$
Nên bốn điểm $B;I;C;K$ nằm trên đường tròn $\left( {O;\dfrac{{IK}}{2}} \right)$.
Tâm của đường tròn đi qua bốn điểm $B,I,C,K$ là

Vì tam giác $ABC$ cân tại $A$ nên $I;K \in $ đường thẳng $AH$ với $\left\{ H \right\} = BC \cap AI$
Ta có $\widehat {HCI} = \dfrac{1}{2}\widehat {HCA};\widehat {KCH} = \dfrac{1}{2}\widehat {xCH}$$ \Rightarrow \widehat {ICK} = \widehat {ICH} + \widehat {HCK} = \dfrac{1}{2}\left( {\widehat {ACH} + \widehat {HCx}} \right) = 90^\circ $
Tương tự ta cũng có $\widehat {IBK} = 90^\circ $
Xét hai tam giác vuông $ICK$ và $IBK$ có $OI = OK = OB = OC = \dfrac{{IK}}{2}$
Nên bốn điểm $B;I;C;K$ nằm trên đường tròn $\left( {O;\dfrac{{IK}}{2}} \right)$.
Kẻ tiếp tuyến với đường tròn tại $C$, tiếp tuyến này cắt đường thẳng $OA$ tại $I$. Biết $OA = R$. Tính $CI$ theo $R$.
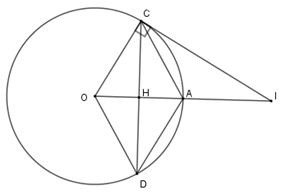
Xét tam giác $COA$ có $OC = OA = R$ và $OC = AC$ (do $OCAD$ là hình thoi) nên $\Delta COA$ là tam giác đều
$ \Rightarrow \widehat {COI} = 60^\circ .$
Xét tam giác vuông $OCI$ có $CI = OC.\tan 60^\circ = R\sqrt 3 $.
Vậy $CI = R\sqrt 3 $.
Tứ giác $OCAD$ là hình gì?

Gọi $H$ là giao của $OA$ và $CD$
Xét $\left( O \right)$ có $OA \bot CD$ tại $H$ nên $H$ là trung điểm của $CD$
Xét tứ giác $OCAD$ có hai đường chéo $OA$ và $CD$ vuông góc với nhau và giao nhau tại trung điểm $H$ mỗi đường nên $OCAD$ là hình thoi.
Tứ giác $OCAD$ là hình gì?

Gọi $H$ là giao của $OA$ và $CD$
Xét $\left( O \right)$ có $OA \bot CD$ tại $H$ nên $H$ là trung điểm của $CD$
Xét tứ giác $OCAD$ có hai đường chéo $OA$ và $CD$ vuông góc với nhau và giao nhau tại trung điểm $H$ mỗi đường nên $OCAD$ là hình thoi.
Tứ giác $ABCE$ là hình gì?
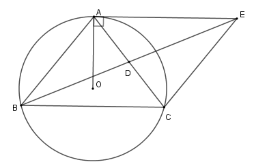
Vì $AE{\rm{//}}BC$ nên $\widehat {EAC} = \widehat {ACB}$ (hai góc ở vị trí so le trong) , lại có $\widehat {ADE} = \widehat {BDC}$ (đối đỉnh) và $AD = DC$
Nên $\Delta ADE = \Delta CDB\left( {g - c - g} \right) $
$\Rightarrow AE = BC$
Tứ giác $AECB$ có $AE = BC;AE{\rm{//}}BC$ nên $AECB$ là hình bình hành.
Chọn khẳng định đúng.

Vì tam giác $ABC$ cân tại $A$ có $O$ là tâm đường tròn ngoại tiếp nên đường thẳng $AO \bot BC$
Lại có $AO \bot AE$ (tính chất tiếp tuyến ) nên $AE{\rm{//}}BC$
Chọn khẳng định đúng.

Vì tam giác $ABC$ cân tại $A$ có $O$ là tâm đường tròn ngoại tiếp nên đường thẳng $AO \bot BC$
Lại có $AO \bot AE$ (tính chất tiếp tuyến ) nên $AE{\rm{//}}BC$
Tâm đường tròn nội tiếp của tam giác là
Tâm của đường tròn nội tiếp tam giác là giao của các đường phân giác các góc trong tam giác.
Mỗi một tam giác có bao nhiêu đường tròn bàng tiếp?
Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với phần kéo dàicủa hai cạnh còn lại gọi là đường tròn bàng tiếp tam giác.
Với một tam giác có ba đường tròn bàng tiếp.
Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Chọn khẳng định sai?
Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:
- Điểm đó cách đều hai tiếp điểm.
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của các góc tạo bởi hai tiếp tuyến.
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.

