Câu hỏi:
3 năm trước
Cho tam giác $ABC$ cân tại $A$ nội tiếp đường tròn $\left( O \right)$. Gọi $D$ là trung điểm cạnh $AC$, tiếp tuyến của đường tròn $\left( O \right)$ tại $A$ cắt tia $BD$ tại $E$.
Tứ giác $ABCE$ là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: a
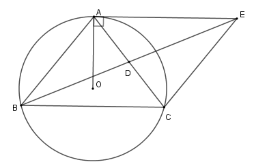
Vì $AE{\rm{//}}BC$ nên $\widehat {EAC} = \widehat {ACB}$ (hai góc ở vị trí so le trong) , lại có $\widehat {ADE} = \widehat {BDC}$ (đối đỉnh) và $AD = DC$
Nên $\Delta ADE = \Delta CDB\left( {g - c - g} \right) $
$\Rightarrow AE = BC$
Tứ giác $AECB$ có $AE = BC;AE{\rm{//}}BC$ nên $AECB$ là hình bình hành.
Hướng dẫn giải:
Sử dụng dấu hiệu nhận biết các hình đặc biệt.

