Câu hỏi:
3 năm trước
Hai tiếp tuyến tại $B$ và $C$ của đường tròn $\left( O \right)$ cắt nhau tại$A$ .
Vẽ đường kính $CD$ của $\left( O \right).$ Khi đó
Trả lời bởi giáo viên
Đáp án đúng: a
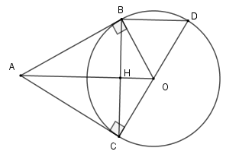
Theo câu trước ta có $AO \bot BC$ (*)
Xét tam giác $BCD$ có $DC$ là đường kính của $\left( O \right)$ và $B \in \left( O \right)$ nên $\Delta BDC$ vuông tại $B$ hay $BD \bot BC$ (**)
Từ (*) và (**) suy ra $BD{\rm{//}}AO$
Mà $AO$ và $AC$ cắt nhau nên $BD$ và $AC$ không thể song song.
Hướng dẫn giải:
Sử dụng quan hệ từ vuông góc đến song song

