Một chất phóng xạ có chu kỳ bán rã T . Thời gian để khối lượng chất phóng xạ còn lại bằng \(\dfrac{{\sqrt 2 }}{4}\) lần khối lượng chất phóng xạ ban đầu là :
\(m = {m_0}{.2^{ - \dfrac{t}{T}}} = \dfrac{{\sqrt 2 }}{4}{m_0} \Leftrightarrow {2^{ - \dfrac{t}{T}}} = {2^{ - 1,5}} \Rightarrow t = 1,5T\)
Một mẫu chất phóng xạ nguyên chất sau thời gian t có số hạt nhân đã phân rã gấp 15 lần số hạt nhân chưa bị phân rã. Khoảng thời gian kể từ lúc số hạt nhân phóng xạ trong mẫu chất này giảm 2 lần cho đến lúc giảm 4 lần là:
- Ta có số hạt nhân đã phân rã gấp 15 lần số hạt nhân chưa bị phân rã:
\(\Delta N = 15N \Leftrightarrow {N_0}\left( {1 - {2^{ - \dfrac{t}{T}}}} \right) = 15.{N_0}{.2^{ - \dfrac{t}{T}}} \Rightarrow t = 4T \Rightarrow T = \dfrac{t}{4}\)
- Thời điểm số hạt nhân phóng xạ trong mẫu giảm đi 2 lần: \({N_0}{.2^{ - \dfrac{{{t_1}}}{T}}} = \dfrac{{{N_0}}}{2} \Rightarrow {t_1} = T\)
- Thời điểm số hạt nhân phóng xạ trong mẫu giảm đi 4 lần: \({N_0}{.2^{ - \dfrac{{{t_2}}}{T}}} = \dfrac{{{N_0}}}{4} \Rightarrow {t_2} = 2T\)
- Khoảng thời gian kể từ lúc số hạt nhân phóng xạ trong mẫu chất này giảm 2 lần cho đến lúc giảm 4 lần: \(\Delta t = {t_2} - {t_1} = T = \dfrac{t}{4}\)
\({}_{11}^{24}Na\) là chất phóng xạ β- với chu kì bán rã 15 h. Ban đầu có một lượng \({}_{11}^{24}Na\) thì sau một khoảng thời gian bao lâu lượng chất phóng xạ trên bị phân rã 64%?
Theo bài ra ta có:
\(\begin{array}{l}\dfrac{{\Delta m}}{{{m_0}}}.100\% = 64\% \\ \Leftrightarrow \dfrac{{{m_0}\left( {1 - {2^{ - \dfrac{t}{T}}}} \right)}}{{{m_0}}} = 0,64\\ \Leftrightarrow 1 - {2^{ - \dfrac{t}{{15}}}} = 0,64\\ \Rightarrow {2^{ - \dfrac{t}{{15}}}} = 0,36 \Rightarrow - \dfrac{t}{{15}} = {\log _2}\left( {0,36} \right)\\ \Rightarrow t \approx 22h\end{array}\)
Một chất phóng xạ có độ phóng xạ ban đầu \({H_0}\), gồm 2 chất phóng xạ có số hạt nhân ban đầu bằng nhau. Chu kì bán rã của chúng lần lượt là \({T_1} = 2h\) và \({T_2} = 3h\). Sau \(6h\), độ phóng xạ của khối chất còn lại là:
Ta có:
+ Độ phóng xạ ban đầu của khối chất:
\(\begin{array}{l}{H_0} = {H_{01}} + {H_{02}} = \dfrac{{\ln 2}}{{{T_1}}}{N_0} + \dfrac{{\ln 2}}{{{T_2}}}{N_0}\\ = \dfrac{{\ln 2}}{2}{N_0} + \dfrac{{\ln 2}}{3}{N_0}\\ \Rightarrow {N_0}\ln 2 = \dfrac{6}{5}{H_0}\end{array}\)
+ Độ phóng xạ tại thời điểm \(t = 6h\) là:
\(\begin{array}{l}H = {H_{01}}{.2^{ - \dfrac{t}{{{T_1}}}}} + {H_{02}}{.2^{ - \dfrac{t}{{{T_2}}}}}\\ = \dfrac{{\ln 2}}{{{T_1}}}{N_0}{.2^{ - \dfrac{t}{{{T_1}}}}} + \dfrac{{\ln 2}}{{{T_2}}}.{N_0}{.2^{ - \dfrac{t}{{{T_2}}}}}\\ = \ln 2.{N_0}\left( {\dfrac{{{2^{ - \dfrac{6}{2}}}}}{2} + \dfrac{{{2^{ - \dfrac{6}{3}}}}}{3}} \right) = \dfrac{6}{5}{H_0}\dfrac{7}{{48}} = \dfrac{{7{H_0}}}{{40}}\end{array}\)
Hạt nhân \({}_{84}^{210}Po\) đứng yên, phân rã α thành hạt nhân chì. Động năng của hạt α bay ra bằng bao nhiêu phần trăm của năng lượng phân rã?
Ta có PTPƯ sau: \({}_{84}^{210}Po \to \alpha + {}_{82}^{206}Pb\)
+ Theo định luật bảo toàn động lượng ta có: \(\overrightarrow {{p_{Po}}} = \overrightarrow {{p_\alpha }} + \overrightarrow {{p_{Pb}}} = 0 \Rightarrow {p_\alpha } = {p_{Pb}}\)
Mà \({p^2} = 2mK \Rightarrow {m_\alpha }{K_\alpha } = {m_{Pb}}{K_{Pb}} \Rightarrow {K_{Pb}} = \dfrac{{{m_\alpha }}}{{{m_{Pb}}}}{K_\alpha }\)
+ Năng lượng phân rã: \(\Delta E = {K_\alpha } + {K_{Pb}} - {K_{Po}} = {K_\alpha } + {K_{Pb}}\)
\(\Delta E = {K_\alpha } + \dfrac{{{m_\alpha }}}{{{m_{Pb}}}}{K_\alpha } = \dfrac{{{m_{Pb}} + {m_\alpha }}}{{{m_{Pb}}}}{K_\alpha } \Rightarrow \dfrac{{{K_\alpha }}}{{\Delta E}} = \dfrac{{{m_{Pb}}}}{{{m_{Pb}} + {m_\alpha }}} = \dfrac{{206}}{{206 + 4}} = 0,981 = 98,1\% \)
Môt hạt nhân X ban đầu đứng yên, phóng xạ α và biến đổi thành hạt nhân con Y. Gọi m1, m2; v1 và v2 ; K1 và K2 tương ứng là khối lượng, tốc độ, động năng của hạt α và hạt Y. Hệ thức đúng là
+ Phương trình phóng xạ: \({}_Z^AX \to {}_2^4\alpha + {}_{Z - 2}^{A - 4}Y\)
+ Bảo toàn động lượng ta có: \(0 = \overrightarrow {{p_\alpha }} + \overrightarrow {{p_\gamma }} \Rightarrow {p_\alpha } = {p_\gamma } \Rightarrow {m_1}{v_1} = {m_2}{v_2} \Rightarrow \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{{m_2}}}{{{m_1}}}(1)\)
+ Lại có: \({p^2} = 2mK \Rightarrow 2{m_1}{K_1} = 2{m_2}{K_2} \Rightarrow \dfrac{{{m_2}}}{{{m_1}}} = \dfrac{{{K_1}}}{{{K_2}}}(2)\)
Từ (1) và (2) \(\frac{{{v_1}}}{{{v_2}}} = \frac{{{m_2}}}{{{m_1}}} = \frac{{{K_1}}}{{{K_2}}}\)
Một hạt nhân có số khối A phóng xạ α. Lấy khối lượng của hạt nhân tính theo đơn vị u bằng số khối của nó. Tỉ số giữa khối lượng hạt nhân con và khối lượng hạt nhân mẹ sau 2 chu kì bán rã
+ Phương trình phóng xạ: \({}_Z^AX \to {}_2^4\alpha + {}_{Z - 2}^{A - 4}Y\)
+ Khối lượng hạt nhân mẹ còn lại sau 2 chu kì là: \({m_X} = {m_0}{.2^{\dfrac{{ - t}}{T}}} = {m_0}{.2^{ - 2}}\)
+ Khối lượng hạt nhân con sinh ra sau 2 chu kì là: \({m_Y} = {m_0}.\dfrac{{{A_{con}}}}{{{A_{me}}}}\left( {1 - {2^{\dfrac{{ - t}}{T}}}} \right) = {m_0}.\dfrac{{A - 4}}{A}\left( {1 - {2^{ - 2}}} \right)\)
Ta có: \(\dfrac{{{m_Y}}}{{{m_X}}} = \dfrac{{\dfrac{{A - 4}}{A}\left( {1 - {2^{ - 2}}} \right){m_0}}}{{{2^{ - 2}}{m_0}}} = \dfrac{{A - 4}}{A}\left( {{2^2} - 1} \right) = \dfrac{{3\left( {A - 4} \right)}}{A}\)
Hạt nhân \({}^{{A_1}}X\)phóng xạ và biến thành một hạt nhân bền \({}^{{A_2}}Y\). Coi khối lượng của các hạt nhân X, Y tính theo đơn vị u bằng số khối của chúng. Biết chất phóng xạ X có chu kì bán rã là T. Ban đầu, có một mẫu X nguyên chất thì sau thời gian 3T, tỉ số giữa khối lượng của chất Y và khối lượng của chất X là
+ Khối lượng Y sinh ra sau 3T: \({m_Y} = {m_{con}} = {m_0}.\dfrac{{{A_{con}}}}{{{A_{me}}}}\left( {1 - {2^{ - 3}}} \right) = {m_0}.\dfrac{{{A_2}}}{{{A_1}}}\left( {1 - {2^{ - 3}}} \right)\)
+ Khối lượng X còn lại sau 3T: \({m_X} = {m_0}{.2^{ - 3}}\)
=> Tỉ số giữa khối lượng của chất Y và khối lượng của chất X là: \(\dfrac{{{m_Y}}}{{{m_X}}} = 7\dfrac{{{A_2}}}{{{A_1}}}\)
Chất pôlôni \({}_{84}^{210}Po\) là phóng xạ hạt \(\alpha\) có chu kỳ bán rã là 138 ngày. Ban đầu giả sử mẫu quặng \(Po\) là nguyên chất và có khối lượng \(210g\), sau \(276\) ngày người ta đem mẫu quặng đó ra cân. Hãy tính khối lượng còn lại của mẫu quặng, coi khối lượng các hạt lấy gần bằng số khối.
+ Phương trình phản ứng : \({}_{84}^{210}Po \to {}^4\alpha + {}^{206}X\)
+ Khối lượng của mẫu quặng sẽ bằng khối lượng còn lại của Po và khối lượng của hạt nhân con X. (Hạt α phân tán ra ngoài môi trường dưới dạng tia phóng xạ).
+ Khối lượng Po còn lại trong mẫu: \({m_{Po}} = {m_0}{.2^{ - \dfrac{t}{T}}} = {210.2^{ - \dfrac{{276}}{{138}}}} = 52,5g\)
+ Khối lượng hạt nhân X sinh ra trong mẫu: \({m_X} = {m_0}.\dfrac{{{A_X}}}{{{A_{Po}}}}\left( {1 - {2^{ - \dfrac{t}{T}}}} \right) = 210.\dfrac{{206}}{{210}}\left( {1 - {2^{ - \dfrac{{276}}{{138}}}}} \right) = 154,5(g)\)
+ Vậy khối lượng của mẫu quặng: \(m{\rm{ }} = {\rm{ }}{m_{Pb}} + {\rm{ }}{m_X} = {\rm{ }}52,5{\rm{ }} + {\rm{ }}154,5{\rm{ }} = {\rm{ }}207\left( g \right)\).
Hạt nhân urani \({}_{92}^{238}U\)sau một chuỗi phân rã, biến đổi thành hạt nhân chì \({}_{82}^{206}Pb\). Trong quá trình đó, chu kì bán rã của \({}_{92}^{238}U\) biến đổi thành hạt nhân chì là 4,47.109 năm. Một khối đá được phát hiện có chứa 1,188.1020 hạt nhân \({}_{92}^{238}U\) và 6,239.1018 hạt nhân \({}_{82}^{206}Pb\). Giả sử khối đá lúc mới hình thành không chứa chì và tất cả lượng chì có mặt trong đó đều là sản phẩm phân rã của \({}_{92}^{238}U\). Tuổi của khối đá từ khi được hình thành cho đến khi được phát hiện là
+ Số hạt nhân U chứa trong mẫu: \({N_U} = {N_0}{.2^{ - \dfrac{t}{T}}} = 1,{188.10^{20}}\)
+ Số hạt nhân con tạo thành: \({N_{Pb}} = \Delta {N_U} = {N_0}.\left( {1 - {2^{ - \dfrac{t}{T}}}} \right) = 6,{239.10^{18}}\)
\(\dfrac{{{N_U}}}{{{N_{Pb}}}} = \dfrac{{{2^{ - \dfrac{t}{T}}}}}{{1 - {2^{ - \dfrac{t}{T}}}}} = \dfrac{{1,{{188.10}^{20}}}}{{6,{{239.10}^{18}}}} \Rightarrow \dfrac{t}{T} = 0,074 \Rightarrow t = 3,{3.10^8}\)năm
Đồng vị \({}_{92}^{238}U\) sau một chuỗi các phân rã thì biến thành chì \({}_{82}^{206}Pb\) bền, với chu kì bán rã \(T = 4,47\) tỉ năm. Ban đầu có một mẫu chất 238U nguyên chất. Sau \(2\) tỉ năm thì trong mẫu chất có lẫn chì 206Pb với khối lượng \({m_{Pb}} = 0,2g\) Giả sử toàn bộ lượng chì đó đều là sản phẩm phân rã từ 238U. Khối lượng 238U ban đầu là
Khối lượng Pb được tạo thành :
\(\begin{array}{l}{m_{Pb}} = {m_{0U}}.\dfrac{{{A_{Pb}}}}{{{A_U}}}.(1 - {2^{ - \dfrac{t}{T}}})\\ = {m_{0U}}.\dfrac{{206}}{{238}}.(1 - {2^{ - \dfrac{t}{T}}})\\ \Rightarrow {m_{0U}} = \dfrac{{{m_{Pb}}.238}}{{\left( {1 - {2^{ - \dfrac{t}{T}}}} \right).206}} = \dfrac{{0,2.238}}{{\left( {1 - {2^{ - \dfrac{2}{{4,47}}}}} \right).206}} = 0,866g\end{array}\)
Một chất phóng xạ \(α\) có chu kì bán rã T. Khảo sát một mẫu chất phóng xạ này ta thấy: ở lần đo thứ nhất, trong 1 phút mẫu chất phóng xạ này phát ra 8n hạt \(α\). Sau 414 ngày kể từ lần đo thứ nhất, trong 1 phút mẫu chất phóng xạ chỉ phát ra n hạt α. Giá trị của T là
+ Số hạt \(α\) phát ra chính là số hạt nhân đã bị phân rã. Gọi \({N_0}\) là số hạt nhân chất phóng xạ trước khi đo lần thứ nhất.
+ Ta có: \(\left\{ \begin{array}{l}\Delta {N_1} = {N_0}(1 - {2^{ - \dfrac{{{t_1}}}{T}}}) = 8n.\\\Delta {N_2} = N{'_0}(1 - {2^{ - \dfrac{{{t_1}}}{T}}}) = n.\end{array} \right.\)
\(\Rightarrow \dfrac{{N'}_0}{{N_0^/}} = 8\)
Lại có: \({N'_0}=N_0.2^{-\dfrac{t}{T}}\)
\(\Rightarrow \dfrac{{{N_0}}}{{{N_0}{{.2}^{-\dfrac{t}{T}}}}} = 8 \Rightarrow {2^{\dfrac{t}{T}}} = {2^3}\)
\(\to T = \dfrac{t}{3} = \dfrac{414}{3}= 138\) (ngày)
Một lượng chất phóng xạ có khối lượng ban đầu là \({m_0}\). Sau 4 chu kỳ bán rã khối lượng chất phóng xạ còn lại là
Khối lượng chất phóng xạ còn lại sau 4 chu kì bán rã là:
\(m = {m_0}{.2^{ - \dfrac{t}{T}}} = {m_0}{.2^{ - \dfrac{{4T}}{T}}} = {m_0}{.2^{ - 4}} = \dfrac{{{m_0}}}{16}\)
Hạt nhân X bị phóng xạ thành hạt nhân bền Y. Hình bên là đồ thị biểu diễn sụ phụ thộc của số hạt nhân X và số hạt nhân Y theo thời gian. Lúc \(t = 6\) ngày, tỷ số giữa hạt nhân X và số hạt nhân Y là:
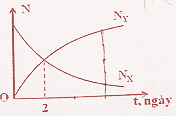
Số hạt nhân X còn lại sau thời gian t là \({N_X} = {N_0}{.2^{ - \dfrac{t}{T}}}\)
Số hạt nhân Y sinh ra sau thời gian t là \({N_Y} = {N_0}\left( {1 - {2^{ - \dfrac{t}{T}}}} \right)\)
Từ đồ thị ta thấy tại \(t = 2\) ngày số hạt nhân X bằng số hạt nhân Y nên ta có
\({N_0}{2^{\dfrac{{-2}}{T}}} = {N_0}\left( {1 - {2^{ - \dfrac{2}{T}}}} \right) = > {2^{-\dfrac{{2}}{T}}} = \dfrac{1}{2} = > - \dfrac{{2}}{T} = - 1 \)
=> \(T = 2\) ngày
Vậy tại \(t = 6\) ngày, tỷ số giữa hạt nhân X và số hạt nhân Y là \(\dfrac{{{N_X}}}{{{N_Y}}} = \dfrac{{{N_0}{{.2}^{\dfrac{{ - 6}}{2}}}}}{{{N_0}\left( {1 - {2^{ - \dfrac{6}{2}}}} \right)}} = \dfrac{{\dfrac{1}{8}}}{{\dfrac{7}{8}}} = \dfrac{1}{7}\)
Ban đầu có \({{N}_{0}}\) hạt nhân của một đồng vị phóng xạ. Tính từ lúc ban đầu, trong khoảng thời gian \(10\) ngày có \(\frac{3}{4}\) số hạt nhân của đồng vị phóng xạ đó đã bị phân rã. Chu kỳ bán rã của đồng vị phóng xạ này là
Số hạt nhân bị phân rã sau \(10\) ngày là:
\(\begin{align}& N={{N}_{0}}\left( 1-{{2}^{-\frac{t}{T}}} \right)=\frac{3}{4}{{N}_{0}}\Rightarrow 1-{{2}^{-\frac{t}{T}}}=\frac{3}{4} \\& \Rightarrow {{2}^{-\frac{t}{T}}}=\frac{1}{4}={{2}^{-2}}\Rightarrow \frac{t}{T}=2\Rightarrow \frac{10}{T}=2\Rightarrow T=5\,\,\left( ngay \right) \\\end{align}\)
Một nhà vật lý hạt nhân làm thí nghiệm xác định chu kỳ bán rã \(\left( T \right)\) của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã \(\left( {\Delta N} \right)\) và số hạt ban đầu \(\left( {{N_0}} \right)\). Dựa vào kết quả thực nghiệm đo được trên hình vẽ, hãy tính \(T\)?
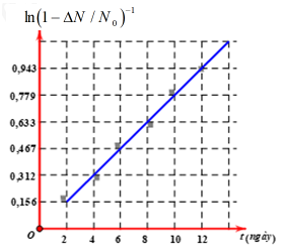
Ta có: \({\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \dfrac{1}{{1 - \dfrac{{\Delta N}}{{{N_0}}}}} = \dfrac{1}{{1 - \left( {1 - {2^{ - \dfrac{t}{T}}}} \right)}} = \dfrac{1}{{{2^{ - \dfrac{t}{T}}}}} = {2^{\dfrac{t}{T}}}\)
\( \Rightarrow \ln {\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \ln \left( {{2^{\dfrac{t}{T}}}} \right)\)
Từ đồ thị ta thấy:
\(\left\{ \begin{array}{l}t = 6ngay\\\ln {\left( {1 - \dfrac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = 0,467\end{array} \right. \Rightarrow \ln \left( {{2^{\dfrac{6}{T}}}} \right) = 0,467 \Rightarrow T = 8,9ngay\)
Trong các biểu thức sau đây, biểu thức nào đúng với nội dung của định luật phóng xạ? (với m0 là khối lượng của chất phóng xạ ban đầu, m là khối lượng chất phóng xạ còn lại tại thời điểm t, $\lambda $ là hằng số phóng xạ).
Khối lượng chất phóng xạ còn lại: \(m = \frac{{{m_0}}}{{{2^{\frac{t}{T}}}}} = {m_0}{2^{ - \frac{t}{T}}} = {m_0}.{e^{ - \lambda t}}\)
Biểu thức xác định số hạt nhân còn lại sau thời gian t là:
Số hạt nhân còn lại: \(N = \frac{{{N_0}}}{{{2^{\frac{t}{T}}}}} = {N_0}{2^{ - \frac{t}{T}}} = {N_0}.{e^{ - \lambda t}}\)
Biểu thức xác định độ phóng xạ của một chất sau thời gian t là:
Độ phóng xạ: \(H = \frac{{{H_0}}}{{{2^{\frac{t}{T}}}}} = {H_0}{2^{ - \frac{t}{T}}} = {H_0}.{e^{ - \lambda t}}\)
Chất Iốt phóng xạ \({}_{53}^{131}\)I dùng trong y tế có chu kỳ bán rã 8 ngày đêm. Nếu nhận được 100g chất này thì sau 8 tuần lễ còn bao nhiêu?
t = 8 tuần = 56 ngày = 7.T .Suy ra sau thời gian t thì khối lượng chất phóng xạ \({}_{53}^{131}\)I còn lại là :
\(m = {m_0}{.2^{ - \frac{t}{T}}} = {100.2^{ - 7}}\)= 0,78 gam .

