Công suất điện tiêu thụ của mạch điện xoay chiều - Hệ số công suất

Ta có:

+ công suất tiêu thụ của mạch điện:

\(P = \dfrac{{{U^2}}}{{{Z^2}}}R\)

+ Do mạch là cuộn dây có điện trở thuần và độ tự cảm L => tổng trở của mạch:

\(Z = \sqrt {{R^2} + {Z_L}^2} \)

\( \to P = \dfrac{{{U^2}}}{{{R^2} + Z_L^2}}R \leftrightarrow 100 = \frac{{{{100}^2}}}{{{{50}^2} + {Z_L}^2}}50 \to {Z_L} = 50\Omega \)

+ Mặt khác, ta có:

\({Z_L} = \omega L = \dfrac{{2\pi }}{T}L \to L = \dfrac{{{Z_L}.T}}{{2\pi }} = \dfrac{{50.0,02}}{{2\pi }} = \dfrac{{0,5}}{\pi }(H)\)

Ta có:

+ Dung kháng:

 \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{2\pi fC}} = \dfrac{1}{{2\pi .50.\dfrac{{{{10}^{ - 3}}}}{{8\pi }}}} = 80\Omega \)

+ Tổng trở của mạch:

\(Z = \sqrt {{R^2} + {Z_C}^2}  = \sqrt {{{60}^2} + {{80}^2}}  = 100\Omega \)

+ hệ số công suất:

\({\rm{cos}}\varphi  = \dfrac{R}{Z} = \dfrac{{60}}{{100}} = 0,6\)

Ta có:

+ \(\begin{array}{l}U = \sqrt {U_R^2 + {{({U_L} - {U_C})}^2}}  \leftrightarrow {U^2} = U_R^2 + {(\frac{U}{2} - U)^2}\\ \to {U_R} = \frac{{\sqrt 3 U}}{2}\end{array}\)

+ Hệ số công suất:

\({\rm{cos}}\varphi  = \frac{R}{Z} = \frac{{{U_R}}}{U} = \frac{{\frac{{\sqrt 3 U}}{2}}}{U} = \frac{{\sqrt 3 }}{2}\)

Điện áp đoạn mạch \(AD\) cùng pha với i nên trên đoạn mạch \(AD\) chỉ có điện trở \(R\) hoặc \(RLC\) nhưng \(Z_L=Z_C\).

\( \to R = \dfrac{U}{I} = 100\Omega \)

Điện áp đoạn mạch \(BD\) sớm pha hơn i một góc \(\varphi  = \dfrac{\pi }{6}\)

=> Trên đoạn mạch \(BD\) có điện trở \(R'\) và X (X có thể là \({Z_L}\) hoặc \({Z_L}\) và \({Z_C}\) \(\left( {{Z_L} > {Z_C}} \right)\)

\(\begin{array}{l} \to \tan \dfrac{\pi }{6} = \dfrac{{{Z_X}}}{{R'}} = \dfrac{1}{{\sqrt 3 }} \to {Z_X} = \dfrac{{R'}}{{\sqrt 3 }}\\ \to {Z_{BD}} = \dfrac{{{U_{BD}}}}{I} = 100\sqrt 3 \end{array}\)

Mặt khác, ta có:

\(\begin{array}{l}{Z_{BD}} = \sqrt {R{'^2} + Z_X^2}  = \sqrt {R{'^2} + \dfrac{{R{'^2}}}{3}}  = \dfrac{{2R'}}{{\sqrt 3 }} = 100\sqrt 3 \\ \Rightarrow R' = 150\Omega \end{array}\)  

=> Công suất tiêu thụ của đoạn mạch AB là: \(P = {I^2}(R + R') = 1(100 + 150) = 250W\)

Hiệu điện thế của đoạn mạch là tổng hợp của 2 thành phần:

+ Phần không đổi: U’=100V phần này không tạo ra dòng điện vì đoạn mạch chứa C ( Tụ điện không cho dòng điện không đổi đi qua)

+ Phần xoay chiều:

\(u = 100\sqrt 2 {\rm{cos(100}}\pi {\rm{t + }}\frac{\pi }{4})V\)

Tổng trở của đoạn mạch là:

 \(Z = 100\sqrt 2  \to I = \frac{1}{{\sqrt 2 }}\)

Công suất tiêu thụ của mạch là:

 \(P = {I^2}R = \frac{1}{2}.100 = 50W\)

 Ta có:

\(\begin{array}{l}L = {R^2}C = {r^2}C\\ =  > {Z_L}.Z_C^{} = {R^2} = {r^2}\end{array}\)

Điện áp hiệu dụng của đoạn mạch RC gấp \(\sqrt 3 \) lần điện áp hiệu dụng hai đầu cuộn dây

\(\begin{array}{l}I.\sqrt {{R^2} + Z_C^2}  = \sqrt 3 .I.\sqrt {{r^2} + Z{{_L^2}^{}}}  <  =  > {R^2} + Z_C^2 = 3({r^2} + Z_L^2)\\ <  =  > {Z_L}.{Z_C} + Z_C^2 = 3.{Z_L}.{Z_C} + 3Z_L^2\\ <  =  > {Z_C}(Z_L^{} + {Z_C}) = 3{Z_L}({Z_L} + {Z_C})\\ =  > {Z_C} = 3{Z_L} =  > {R^2} = 3Z_L^2 =  > R = Z{}_L\sqrt 3 \end{array}\)

=> Hệ số công suất của đoạn mạch là

\(\cos \varphi  = \frac{{R + r}}{{\sqrt {{{(R + r)}^2} + {{({Z_L} - Zc)}^2}} }} = \frac{{2R}}{{\sqrt {4{R^2} + 4Z_L^2} }} = \frac{{2\sqrt 3 {Z_L}}}{{\sqrt {4.3.Z_L^2 + 4Z_L^2} }} = \frac{{\sqrt 3 }}{2}\)

+  Mạch R₁,L: \(\tan {\varphi _1} = \dfrac{{{Z_L}}}{{{R_1}}} = \tan \dfrac{\pi }{6} = \dfrac{1}{{\sqrt 3 }} \to {R_1} = {Z_L}\sqrt 3  \to {Z_1} = \dfrac{{2{R_1}}}{{\sqrt 3 }}(*).\)

+  Mạch R₂,C: \(\tan {\varphi _2} = \dfrac{{ - {Z_C}}}{{{R_2}}} = \tan \dfrac{{ - \pi }}{4} =  - 1 \to {R_2} = {Z_C} \to {Z_2} = {R_2}\sqrt 2 (**).\)

+ Mạch R₁,L và mạch R₂, C: Cùng U, có cùng I à \({Z_1}\)= \({Z_2}\), từ (*) và (**) à \({R_1} = {R_2}\sqrt {\dfrac{3}{2}} \).

+ Chuẩn hóa: \({R_2} = 1 \to {Z_C} = 1 \to {R_1} = \sqrt {\dfrac{3}{2}}  \to {Z_L} = \dfrac{1}{{\sqrt 2 }}.\)

+ Mạch gồm R₁, R₂, L và C mắc nối tiếp thì hệ số công suất:  \({\rm{cos}}\varphi  = \dfrac{{{R_1} + {R_2}}}{{\sqrt {{{({R_1} + {R_2})}^2} + {{({Z_L} - {Z_C})}^2}} }} \approx \)\(0,991\)

Khi dòng điện có tần số góc \(\omega = \frac{1}{{\sqrt {LC} }}\) chạy qua đoạn mạch thì trong mạch xảy ra cộng hưởng điện.

Hệ số công suất bằng: 

\(\cos \varphi = \frac{R}{Z} = \frac{R}{R} = 1\)

Hai giá trị dung kháng của tụ điện là:

\(\left\{ \begin{array}{l}{Z_{{C_1}}} = \dfrac{1}{{2\pi f{C_1}}} = \dfrac{1}{{2\pi .50.\dfrac{{{{1.10}^{ - 3}}}}{{20\pi }}}} = 200\,\,\left( \Omega  \right)\\{Z_{{C_2}}} = \dfrac{1}{{2\pi f{C_2}}} = \dfrac{1}{{2\pi .50.\dfrac{{{{1.10}^{ - 3}}}}{{40\pi }}}} = 400\,\,\left( \Omega  \right)\end{array} \right.\)

Công suất trên mạch có giá trị bằng nhau, ta có:

\(\begin{array}{l}P = \dfrac{{{U^2}.R}}{{{R^2} + {{\left( {{Z_L} - {Z_{{C_1}}}} \right)}^2}}} = \dfrac{{{U^2}.R}}{{{R^2} + {{\left( {{Z_L} - {Z_{{C_2}}}} \right)}^2}}}\\ \Rightarrow \left| {{Z_L} - {Z_{{C_1}}}} \right| = \left| {{Z_L} - {Z_{{C_2}}}} \right| \Rightarrow \left| {{Z_L} - 400} \right| = \left| {{Z_L} - 200} \right| \Rightarrow {Z_L} = 300\,\,\left( \Omega  \right)\end{array}\)

Mặt khác: \({Z_L} = 2\pi fL \Rightarrow 300 = 2.50\pi .L \Rightarrow L = \dfrac{3}{\pi }\,\,\left( H \right)\)

Dung kháng của tụ điện là: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\,\,\left( \Omega  \right)\)

Công suất trong mạch đạt cực đại khi:

\({Z_L} = {Z_C} = 100\,\,\left( \Omega  \right) \Rightarrow \omega L = 100 \Rightarrow 100\pi L = 100 \Rightarrow L = \dfrac{1}{\pi }\,\,\left( H \right)\)

Ta có hiệu điện thế giữa hai đầu đoạn mạch là:

\(\begin{array}{l}{u_{AB}} = {u_{AD}} + {u_{DB}} = 100\sqrt 2 \angle \dfrac{\pi }{2} + 100\sqrt 6 \angle \dfrac{{2\pi }}{3} = 100\sqrt {14} \angle 1,9\\ \Rightarrow \left\{ \begin{array}{l}{U_{0AB}} = 100\sqrt {14} \,\,\left( V \right) \Rightarrow {U_{AB}} = \dfrac{{{U_{0AB}}}}{{\sqrt 2 }} = \dfrac{{100\sqrt {14} }}{{\sqrt 2 }} = 100\sqrt 7 \,\,\left( V \right)\\{\varphi _u} = 1,9\,\,\left( {rad} \right) \Rightarrow \Delta \varphi  = {\varphi _u} - {\varphi _i} = 1,9 - \dfrac{\pi }{2} = 0,33\,\,\left( {rad} \right) = 18,{86^0}\end{array} \right.\end{array}\)

Công suất tiêu thụ của đoạn mạch là:

\(P = UI\cos \Delta \varphi  = 100\sqrt 7 .1.cos18,86 = 250\,\,\left( W \right)\)

Áp dụng công thức tính công suất của quạt:

\(P = U.I.\cos \varphi \Rightarrow I = \frac{P}{{U.\cos \varphi }} = \frac{{80}}{{220.0,8}} = \frac{5}{{11}}A\)

Mạch điện có giản đồ vecto:

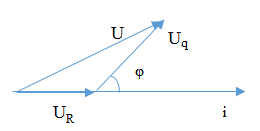
Từ đó ta tìm được U_R từ giản đồ vecto:

\(\begin{gathered}
U = \sqrt {U_R^2 + U_q^2 - 2{U_R}.{U_q}.\cos ({{180}^0} - \varphi )} \hfill \\
\Leftrightarrow {380^2} = U_R^2 + {220^2} - 2.{U_R}.220.( - \cos \varphi ) \Rightarrow {U_R} = 180V \hfill \\
\end{gathered} \)

Xác định được điện trở R:

\(R = \frac{{{U_R}}}{I} = \frac{{180}}{{\frac{5}{{11}}}} = {396_{}}\Omega \)

Đoạn mạch AM có:

\(\left\{ \begin{array}{l}{R_1} = 40\Omega \\{Z_C} = \dfrac{1}{{\omega C}} = 40\Omega \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{Z_{AM}} = 40\sqrt 2 \Omega \\\tan {\varphi _{AM}} =  - \dfrac{{{Z_C}}}{{{R_1}}} =  - 1 \Rightarrow {\varphi _{uAM}} - {\varphi _i} =  - \dfrac{\pi }{4}\end{array} \right.\)

Dòng điện hiệu dụng chạy qua mạch:

\(I = \dfrac{{{U_{AM}}}}{{{Z_{AM}}}} = \dfrac{{50}}{{40\sqrt 2 }} = \dfrac{{5\sqrt 2 }}{8}A\)

Từ hai biểu thức của điện áp tức thời ở hai đầu đoạn mạch AM và MB ta có:

\({\varphi _{uMB}} - {\varphi _{uAM}} = \dfrac{{7\pi }}{{12}} \Rightarrow {\varphi _{uAM}} = {\varphi _{uMB}} - \dfrac{{7\pi }}{{12}}\)

Mà: \({\varphi _{uAM}} - {\varphi _i} =  - \dfrac{\pi }{4} \Rightarrow {\varphi _{uMB}} - \dfrac{{7\pi }}{{12}} - {\varphi _i} =  - \dfrac{\pi }{4} \Rightarrow {\varphi _{uMB}} - {\varphi _i} = \dfrac{\pi }{3}\)

\( \Rightarrow \tan {\varphi _{MB}} = \tan \dfrac{\pi }{3} = \dfrac{{{Z_L}}}{{{R_2}}} \Rightarrow {Z_L} = \sqrt 3 .{R_2}\,\,\,\left( 1 \right)\)

Lại có: \({Z_{MB}} = \dfrac{{{U_{MB}}}}{I} = \dfrac{{75\sqrt 2 }}{{\dfrac{{5\sqrt 2 }}{8}}} = 120 \Rightarrow \sqrt {R_2^2 + Z_L^2}  = 120\,\,\left( 2 \right)\)

Từ (1) và (2) suy ra: \(\left\{ \begin{array}{l}{R_2} = 60\Omega \\{Z_L} = 60\sqrt 3 \Omega \end{array} \right.\)

Hệ số công suất của đoạn mạch:

\(\begin{array}{l}\cos \varphi  = \dfrac{{{R_1} + {R_2}}}{{\sqrt {{{\left( {{R_1} + {R_2}} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\\ \Rightarrow \cos \varphi  = \dfrac{{40 + 60}}{{\sqrt {{{\left( {40 + 60} \right)}^2} + {{\left( {60\sqrt 3  - 40} \right)}^2}} }} = 0,84\end{array}\)

Ta có: \(\left( {{u_d},u} \right) = 1,56rad = \frac{\pi }{2};U = 6V;{U_d} = 10V\)

Vì điện áp hai đầu cuộn dây lệch pha với điện áp hai đầu đoạn mạch góc 1,56rad nên cuộn dây có điện trở thuần.

Ta có giản đồ vecto:

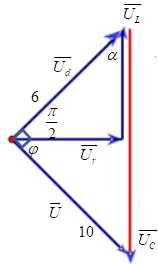
Từ giản đồ vecto ta có: \(\tan \alpha  = \frac{6}{{10}} = 0,6\)

\( \Rightarrow \alpha  = shif\tan 0,6 = 0,54042\) \( \Rightarrow \cos \alpha  = 0,86\)

Mà \(\alpha  = \varphi  \Rightarrow \cos \varphi  = 0,86\)

Công suất tiêu thụ của đoạn mạch \(AB\) là:

 \(P = \dfrac{{{U^2}}}{R}.co{s^2}\varphi  = \dfrac{{{{220}^2}}}{{100}}.{\left( {\cos \dfrac{\pi }{3}} \right)^2} = 121W\)

Công suất hao phí trên đường dây: \({P_{hp}} = \frac{{{P^2}}}{{{U^2}co{{\rm{s}}^2}\varphi }}R\)

Ta có: \(H = \frac{{{U_N}}}{E} = \frac{{{R_N}}}{{{R_N} + r}}\)

Từ đồ thị ta có tại \(R = 3\Omega \) thì \(H = 0,75\)

\( \Leftrightarrow \frac{R}{{R + r}} = 0,75 \Leftrightarrow \frac{3}{{3 + r}} = 0,75 \Rightarrow r = 1\Omega \)

Công suất tiêu thụ trên R:

\({P_R} = {I^2}R = \frac{{{E^2}}}{{{{\left( {R + r} \right)}^2}}}R = \frac{{{E^2}}}{{{{\left( {\sqrt R  + \frac{r}{{\sqrt R }}} \right)}^2}}}\)

\( \Rightarrow {P_{Rma{\rm{x}}}}\) khi \({\left( {\sqrt R  + \frac{r}{{\sqrt R }}} \right)^2}_{\min }\)

Áp dụng BĐT Cosi ta có: \(\sqrt R  + \frac{r}{{\sqrt R }} \ge 2\sqrt r  = 2\)

\( \Rightarrow \sqrt R  + \frac{r}{{\sqrt R }} = 2\sqrt r  = 2\) khi \(\sqrt R  = \frac{r}{{\sqrt R }}\)hay \(R = r\)

\( \Rightarrow {P_{R\max }} = \frac{{{E^2}}}{{4{\rm{R}}}} = \frac{{{E^2}}}{{4{\rm{r}}}} = \frac{{{6^2}}}{4} = 9W\)

Từ đồ thị ta có:

Khi \(\varphi  = 0 \to {P_{ma{\rm{x}}}} = {P_0} = \frac{{{U^2}}}{R}\,\,\,\,\left( 1 \right)\)

Khi \(\varphi  = {\varphi _1} \to P = \frac{3}{4}{P_0} = UI\cos \varphi  = \frac{{{U^2}}}{{{Z^2}}}R\,\,\,\,\,\left( 2 \right)\)

Từ (1) và (2) ta suy ra: \(\frac{3}{4}\frac{{{U^2}}}{R} = \frac{{{U^2}}}{{{Z^2}}}R\)

\( \Rightarrow 3{{\rm{Z}}^2} = 4{{\rm{R}}^2} \Leftrightarrow 3\left( {{R^2} + Z_L^2} \right) = 4{{\rm{R}}^2} \Rightarrow {Z_L} = \frac{R}{{\sqrt 3 }}\)

Lại có: \(\tan {\varphi _1} = \frac{{{Z_L}}}{R} = \frac{1}{{\sqrt 3 }} \Rightarrow {\varphi _1} = \frac{\pi }{6}\) rad

Cường độ dòng điện hiệu dụng trong mạch là:

\(I = \dfrac{P}{{U\cos \varphi }} = \dfrac{{1200}}{{220.1}} = \dfrac{{60}}{{11}} \approx 5,45\left( A \right)\)

Khi mắc điện áp u vào hai đầu đoạn mạch X, độ lệch pha giữa điện áp và cường độ dòng điện là:

\(\tan \varphi  = \dfrac{{{Z_{L1}} - {Z_{C1}}}}{{{R_1}}} = \tan \dfrac{\pi }{6} = \dfrac{{\sqrt 3 }}{3} \Rightarrow {Z_{L1}} - {Z_{C1}} = \dfrac{{\sqrt 3 }}{3}{R_1}\)

Chuẩn hóa \({R_1} = 1 \Rightarrow {Z_{L1}} - {Z_{C1}} = \dfrac{{\sqrt 3 }}{3}\)

Công suất tiêu thụ trên đoạn mạch X là:

\(\begin{array}{l}P = \dfrac{{{U_{R1}}^2}}{{{R_1}}} = \dfrac{{{{\left( {U.cos\varphi } \right)}^2}}}{{{R_1}}} \Rightarrow \frac{{{U^2}.{{\left( {\dfrac{{\sqrt 3 }}{2}} \right)}^2}}}{{{R_1}}} = 250\sqrt 3 \\ \Rightarrow {U^2} = \dfrac{{1000\sqrt 3 }}{3}{R_1} = \dfrac{{1000\sqrt 3 }}{3}\end{array}\)

Khi mắc điệu áp u vào hai đầu đoạn mạch X, Y mắc nối tiếp

Điện áp giữa hai đầu đoạn mạch X và Y vuông pha, ta có:

\(\begin{array}{l}\tan {\varphi _1}.\tan {\varphi _2} =  - 1 \Rightarrow \dfrac{{{Z_{L1}} - {Z_{C1}}}}{{{R_1}}}.\dfrac{{{Z_{L2}} - {Z_{C2}}}}{{{R_2}}} =  - 1\\ \Rightarrow \frac{{\sqrt 3 }}{3}.\dfrac{{{Z_{L2}} - {Z_{C2}}}}{{{R_2}}} =  - 1 \Rightarrow {Z_{L2}} - {Z_{C2}} =  - \sqrt 3 {R_2}\end{array}\)

Cường độ dòng điện trong mạch là:

\(I = \dfrac{U}{{\sqrt {{{\left[ {\left( {{Z_{L1}} - {Z_{C1}}} \right) + \left( {{Z_{L2}} - {Z_{C2}}} \right)} \right]}^2} + {{\left( {{R_1} + {R_2}} \right)}^2}} }}\)

\( \Rightarrow I = \dfrac{U}{{\sqrt {{{\left( {\dfrac{{\sqrt 3 }}{3} - \sqrt 3 {R_2}} \right)}^2} + {{\left( {1 + {R_2}} \right)}^2}} }} = \dfrac{U}{{\sqrt {\dfrac{4}{3} + 4{R_2}^2} }}\)

Công suất tiêu thụ của đoạn mạch X là:

\(\begin{array}{l}{P_1} = {I^2}{R_1} = \dfrac{{{U^2}{R_1}}}{{\dfrac{4}{3} + 4{R_2}^2}} = 90\sqrt 3 \\ \Rightarrow \dfrac{{\dfrac{{1000\sqrt 3 }}{3}}}{{\dfrac{4}{3} + 4{R_2}^2}} = 90\sqrt 3  \Rightarrow {R_2}^2 = \dfrac{{16}}{{27}} \Rightarrow {R_2} = \dfrac{4}{{3\sqrt 3 }}\end{array}\)

Công suất tiêu thụ trên đoạn mạch Y là:

\({P_2} = {I^2}{R_2} = \dfrac{{{U^2}{R_2}}}{{\dfrac{4}{3} + 4{R_2}^2}} = \dfrac{{\dfrac{{1000\sqrt 3 }}{3}.\dfrac{4}{{3\sqrt 3 }}}}{{\dfrac{4}{3} + 4.\dfrac{{16}}{{27}}}} = 120\,\,\left( {\rm{W}} \right)\)