Câu hỏi:
2 năm trước
Một quạt điện xoay chiều mắc nối tiếp với điện trở R rồi mắc hai đầu đoạn mạch này vào điện áp xoay chiều có giá trị hiệu dụng 380 V. Biết quạt điện này có giá trị định mức 220V – 80 W và khi hoạt động đúng công suất định mức thì độ lệch pha giữa điện áp ở hai đầu quạt và cường độ dòng điện chạy qua nó là φ với cosφ = 0,8. Để quạt điện chạy gần đúng công suất định mức nhất thì R có giá trị
Trả lời bởi giáo viên
Đáp án đúng: c
Áp dụng công thức tính công suất của quạt:
\(P = U.I.\cos \varphi \Rightarrow I = \frac{P}{{U.\cos \varphi }} = \frac{{80}}{{220.0,8}} = \frac{5}{{11}}A\)
Mạch điện có giản đồ vecto:
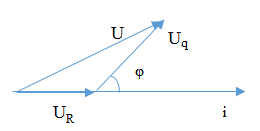
Từ đó ta tìm được UR từ giản đồ vecto:
\(\begin{gathered}
U = \sqrt {U_R^2 + U_q^2 - 2{U_R}.{U_q}.\cos ({{180}^0} - \varphi )} \hfill \\
\Leftrightarrow {380^2} = U_R^2 + {220^2} - 2.{U_R}.220.( - \cos \varphi ) \Rightarrow {U_R} = 180V \hfill \\
\end{gathered} \)
Xác định được điện trở R:
\(R = \frac{{{U_R}}}{I} = \frac{{180}}{{\frac{5}{{11}}}} = {396_{}}\Omega \)
Hướng dẫn giải:
Ta coi đoạn mạch gồm R nối tiếp quạt là điện trở R nối tiếp với đọan mạch RLC nối tiếp.
Áp dụng công thức tính công suất của quạt \(P = U.I.\cos \varphi \) ta tính được cường độ dòng điện I
Vẽ giản đồ vecto của đoạn mạch.
Từ đó ta tìm được UR từ giản đồ vecto:
\(U = \sqrt {U_R^2 + U_q^2 - 2{U_R}.{U_q}.\cos ({{180}^0} - \varphi )} \)
Xác định được điện trở R:
\(R = \frac{{{U_R}}}{I}\)
Câu hỏi khác
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
