Trên mặt nước có hai nguồn sóng nước giống nhau cách nhau $AB = 8(cm)$. Sóng truyền trên mặt nước có bước sóng $1,2 (cm)$. Số đường cực đại đi qua đoạn thẳng nối hai nguồn là:
Do $A, B$ dao động cùng pha nên số đường cực đại trên AB thoã mãn:
\(\dfrac{{ - L}}{\lambda } < k < \dfrac{L}{\lambda }\)
Thay số ta có :
\(\dfrac{{ - 8}}{{1,2}} < k < \dfrac{8}{{1,2}} \Leftrightarrow - 6,67 < k < 6,67\)
\( \to k = \pm 6, \pm 5, \pm 4, \pm 3, \pm 2, \pm 1,0\) .
Hai nguồn sóng cơ $AB$ cách nhau dao động chạm nhẹ trên mặt chất lỏng, cùng tấn số $100Hz$, cùng pha theo phương vuông vuông góc với mặt chất lỏng. Vận tốc truyền sóng $20m/s$.Số điểm không dao động trên đoạn $AB = 1m$ là :
Ta có:
Bước sóng:
\(\lambda = \dfrac{v}{f} = \dfrac{{20}}{{100}} = 0,2m\)
A, B dao động cùng pha => Số điểm không dao động (cực tiểu) trên AB thỏa mãn:
\(\begin{array}{l}\dfrac{{ - L}}{\lambda } - \dfrac{1}{2} < k < \dfrac{L}{\lambda } - \dfrac{1}{2} \leftrightarrow - \dfrac{1}{{0,2}} - \dfrac{1}{2} < k < \dfrac{1}{{0,2}} - \dfrac{1}{2}\\ \to - 5,5 < k < 4,5\\ \to k = - 5; \pm 4, \pm 3; \pm 2; \pm 1,0\end{array}\)
=> Có $10$ điểm
Hai nguồn kết hợp $A, B$ cách nhau $45 mm$ ở trên mặt thoáng chất lỏng dao động theo phương trình $u_1 = u_2 = 2cos100πt (mm)$. Trên mặt thoáng chất lỏng có hai điểm $M$ và $M’$ ở cùng một phía của đường trung trực của $AB$ thỏa mãn: $MA - MB = 15 mm$ và $M’A - M’B = 35 mm$. Hai điểm đó đều nằm trên các vân giao thoa cùng loại và giữa chúng chỉ có một vân loại đó. Vận tốc truyền sóng trên mặt chất lỏng là:
- Giả sử $M$ và $M’$ thuộc vân cực đại.
Khi đó:
+ $MA – MB = 15mm = kλ$
+ $M’A – M’B = 35mm = (k + 2)λ$
\( \to \dfrac{{MA - MB}}{{M'A - M'B}} = \dfrac{k}{{k + 2}} = \dfrac{3}{7} \to k = 1,5\) không thoả mãn (do k ∈ Z)
=> $M$ và $M’$ không thuộc vân cực đại.
- Nếu $M, M’$ thuộc vân cực tiểu thì:
\(MA-MB = 15mm = \left( {2k{\rm{ }} + {\rm{ }}1} \right)\dfrac{\lambda }{2}\)
\(M'A-M'B{\text{ }} = 35mm = \left[ {2\left( {k + 2} \right) + 1} \right]\dfrac{\lambda }{2}\)
\( \to \dfrac{{MA - MB}}{{M'A - M'B}} = \dfrac{{2k + 1}}{{2k + 5}} = \dfrac{3}{7} \to k = 1\)
Vậy $M, M’$ thuộc vân cực tiểu thứ $2$ và thứ $4$
\(\begin{array}{l} \to MA-MB = 15mm = \left( {2k{\rm{ }} + {\rm{ }}1} \right)\dfrac{\lambda }{2} = \dfrac{{3\lambda }}{2}\\ \to \lambda = 10mm = \dfrac{v}{f} \to v = \lambda f = 10.\dfrac{{100\pi }}{{2\pi }} = 500mm/s = 0,5m/s\end{array}\)
Tại hai điểm A,B trên mặt chất lỏng cách nhau 10(cm) có hai nguồn phát sóng theo phương thẳng đứng với các phương trình : \({u_1} = 0,2.cos(50\pi t)cm\) và\({u_1} = 0,2.cos(50\pi t + \pi )cm\) . Vận tốc truyền sóng là 0,5 (m/s). Coi biên độ sóng không đổi. Xác định số điểm dao động với biên độ cực đại trên đoạn thẳng AB ?
Bước sóng :
\(\lambda = vT = v\frac{{2\pi }}{\omega } = 0,5.\frac{{2\pi }}{{50\pi }} = 0,02(m) = 2cm\).
Ta thấy A, B là hai nguồn dao động ngược pha nên số điểm dao động cực đại thoã mãn :
\(\begin{array}{l}\frac{{ - AB}}{\lambda } - \frac{1}{2} < k < \frac{{AB}}{\lambda } - \frac{1}{2}\\ \to \frac{{ - 10}}{2} - \frac{1}{2} < k < \frac{{10}}{2} - \frac{1}{2} \to - 5,5 < k < 4,5\\ \to k = - 5; \pm 4; \pm 3; \pm 2; \pm 1;0\end{array}\).
=> Có 10 điểm
Hai nguồn sóng cùng biên độ cùng tần số và ngược pha. Nếu khoảng cách giữa hai nguồn là: \(AB = 16,2\lambda \) thì số điểm đứng yên và số điểm dao động với biên độ cực đại trên đoạn $AB$ lần lượt là:
Do hai nguồn dao động ngược pha nên số điểm đứng yên trên đoạn AB là :
\(\begin{array}{l}\dfrac{{ - AB}}{\lambda } < k < \dfrac{{AB}}{\lambda } \leftrightarrow \dfrac{{ - 16,2\lambda }}{\lambda } < k < \dfrac{{16,2\lambda }}{\lambda }\\ - 16,2{\rm{ }} < {\rm{ }}k{\rm{ }} < {\rm{ }}16,2.\end{array}\)
=> Có $33$ điểm đứng yên (cực tiểu)
Số điểm cực đại là :
\(\begin{array}{l}\dfrac{{ - AB}}{\lambda } - \dfrac{1}{2} < k < \dfrac{{AB}}{\lambda } - \dfrac{1}{2} \leftrightarrow \dfrac{{ - 16,2\lambda }}{\lambda } - \dfrac{1}{2} < k < \dfrac{{16,2\lambda }}{\lambda } - \dfrac{1}{2}\\ - 16,7 < k < 15,7\end{array}\)
=> Có $32$ điểm cực đại
Trên mặt nước có hai nguồn kết hợp $A,B$ cách nhau $10 (cm)$ dao động theo các phương trình : \({u_1} = 0,2.cos(50\pi t + \pi )cm\) và : \({u_1} = 0,2.cos(50\pi t + \dfrac{\pi }{2})cm\). Biết vận tốc truyền sóng trên mặt nước là $0,5 (m/s)$. Tính số điểm cực đại và cực tiểu trên đoạn $A,B$.
Bước sóng :
\(\lambda = vT = v\dfrac{{2\pi }}{\omega } = 0,5.\dfrac{{2\pi }}{{50\pi }} = 0,02(m) = 2cm\)
Nhìn vào phương trình ta thấy $A, B$ là hai nguồn dao động vuông pha nên số điểm dao động cực đại và cực tiểu là bằng nhau và thoã mãn :
\(\begin{array}{l}\dfrac{{ - AB}}{\lambda } - \dfrac{1}{4} < k < \dfrac{{AB}}{\lambda } - \dfrac{1}{4} \leftrightarrow \dfrac{{ - 10}}{2} - \dfrac{1}{4} < k < \dfrac{{10}}{2} - \dfrac{1}{4}\\ - 5,25 < k < 4,75\end{array}\)
=> Có $10$ điểm dao động với biên độ cực đại và $10$ điểm dao động cực tiểu.
Trên mặt nước, hai nguồn kết hợp $A, B$ cách nhau $40cm$ luôn dao động cùng pha, có bước sóng $6cm$. Hai điểm $CD$ nằm trên mặt nước mà $ABCD$ là một hình chữ nhật, $AD = 30cm$. Số điểm cực đại và đứng yên trên đoạn $CD$ lần lượt là :
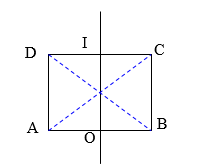
\(BD = AD = \sqrt {A{B^2} + A{D^2}} = 50cm\)
Cách 1 :
Bước 1: Số điểm cực đại trên đoạn $DI$ thoã mãn :
\({d_2} - {d_1} = k\lambda \Rightarrow k = \dfrac{{{d_2} - {d_1}}}{\lambda } = \dfrac{{BD - AD}}{\lambda } = \dfrac{{50 - 30}}{6} = 3,33\) Với k thuộc $Z$ lấy $k=3$
Vậy số điểm cực đại trên đoạn $CD$ là : $k’=2.k + 1=3.2 + 1=7$
Bước 2 : Số điểm cực tiểu trên đoạn $DI$ thoã mãn :
\({d_2} - {d_1} = (2k + 1)\dfrac{\lambda }{2} \Rightarrow 2k + 1 = \dfrac{{2({d_2} - {d_1})}}{\lambda } = \dfrac{{2(BD - AD)}}{\lambda } = \dfrac{{2(50 - 30)}}{6} = 6,67\) .
Giải suy ra $k = 2,83$ (Với k thuộc Z) nên lấy $k=3$ ( vì \(k = 2,83 > 2,5\) ta lấy cận trên là $3$)
Vậy số điểm cực tiểu trên đoạn $CD$ là : $k’ = 2.k = 2.3 = 6$
Cách 2 :
Do hai nguồn dao động cùng pha nên số điểm dao động với biên độ cực đại trên đoạn $CD$ thoã mãn :
Số điểm cực đại trên đoạn $CD$ thoã mãn :
\(\left\{ \begin{array}{l}{d_2} - {d_1} = k\lambda \\AD - BD < {d_2} - {d_1} < AC - BC\end{array} \right.\)
Suy ra :
\(AD - BD < k\lambda < AC - BC\) Hay : \(\dfrac{{AD - BD}}{\lambda } < k < \dfrac{{AC - BC}}{\lambda }\). Hay : \(\dfrac{{30 - 50}}{6} < k < \dfrac{{50 - 30}}{6}\)
Giải ra : $-3,3<k<3,3$
Kết luận có $7$ điểm cực đại trên $CD$.
Số điểm cực tiểu trên đoạn $CD$ thoã mãn :
\(\left\{ \begin{array}{l}{d_2} - {d_1} = (2k + 1)\dfrac{\lambda }{2}\\AD - BD < {d_2} - {d_1} < AC - BC\end{array} \right.\)
Suy ra :
\(AD - BD < (2k + 1)\dfrac{\lambda }{2} < AC - BC\) Hay : \(\dfrac{{2(AD - BD)}}{\lambda } < 2k + 1 < \dfrac{{2(AC - BC)}}{\lambda }\). Thay số :
\(\dfrac{{2(30 - 50)}}{6} < 2k + 1 < \dfrac{{2(50 - 30)}}{6}\) Suy ra : \( - 6,67 < 2k + 1 < 6,67\)
Vậy : $-3,8 < k < 2,835$. Kết luận có 6 điểm đứng yên.
Tại 2 điểm A, B cách nhau 13cm trên mặt nước có 2 nguồn sóng đồng bộ, tạo ra sóng mặt nước có bước sóng là 1,2cm. M là điểm trên mặt nước cách A và B lần lượt là 12cm và 5cm .N đối xứng với M qua AB. Số hyperbol cực đại cắt đoạn MN là :
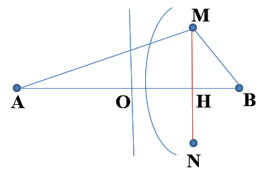
Ta có: \(A{M^2} + M{B^2} = A{B^2}\) \( \Rightarrow \Delta AMB\) vuông tại M.
Từ hình vẽ ta có: \(\cos \angle \left( {{\rm{MAB}}} \right) = {\rm{cos}}\angle \left( {{\rm{MAH}}} \right)\)
\( \Leftrightarrow \dfrac{{AM}}{{AB}} = \dfrac{{AH}}{{AM}} \Rightarrow AH = \dfrac{{A{M^2}}}{{AB}} = \dfrac{{{{12}^2}}}{{13}} = \dfrac{{144}}{{13}}cm\)
Lại có: \(HB = AB - AH = 13 - \dfrac{{144}}{{13}} = \dfrac{{25}}{{13}}cm\)
Số cực đại trên HM thỏa mãn:
\(\begin{array}{l}AH - HB > {d_2} - {d_1} = k\lambda > AM - MB\\ \Leftrightarrow \dfrac{{144}}{{13}} - \dfrac{{25}}{{13}} > 1,2k > 12 - 5 \Leftrightarrow 7,63 > k > 5,83 \Rightarrow k = 6,7\end{array}\)
Vậy có 2 hyperbol cực đại cắt MN.
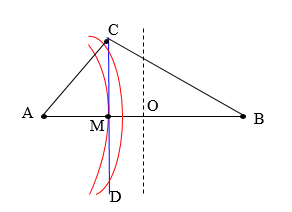
Trên mặt nước có hai nguồn sóng giống nhau A và B, hai nguồn cùng pha, cách nhau khoảng \(AB = 10 cm\) đang dao động vuông góc với mặt nước tạo ra sóng có bước sóng \(λ= 0,5 cm\). C và D là hai điểm khác nhau trên mặt nước, CD vuông góc với AB tại M sao cho \(MA = 3 cm\); \(MC = MD = 4 cm\). Số điểm dao động cực đại trên CD là:

Ở mặt thoáng của một chất lỏng có hai nguồn kết hợp $A$ và $B$ cách nhau $20(cm)$ dao động theo phương thẳng đứng với phương trình \({u_A} = 2.cos(40\pi t)(mm)\) và \({u_B} = 2.cos(40\pi t + \pi )(mm)\). Biết tốc độ truyền sóng trên mặt chất lỏng là $30(cm/s)$. Xét hình vuông $ABCD$ thuộc mặt chất lỏng. Số điểm dao động với biên độ cực đại trên đoạn $BD$ là :
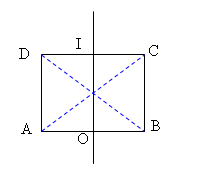
\(BD = \sqrt {A{D^2} + A{B^2}} = 20\sqrt 2 (cm)\)
Với \(\omega = 40\pi (rad/s) \Rightarrow T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{40\pi }} = 0,05(s)\)
Vậy :
\(\lambda = v.T = 30.0,05 = 1,5cm\)
Tìm số điểm dao động với biên độ cực đại trên đoạn $DB$ chứ không phải $DC$.
Nghĩa là điểm $C$ lúc này đóng vai trò là điểm $B$.
Do hai nguồn dao động ngược pha nên số cực đại trên đoạn $BD$ thoã mãn :
\(\left\{ \begin{array}{l}{d_2} - {d_1} = (2k + 1)\dfrac{\lambda }{2}\\AD - BD < {d_2} - {d_1} < AB - 0\end{array} \right.\)
Suy ra :
\(AD - BD < (2k + 1)\dfrac{\lambda }{2} < AB\) Hay : \(\dfrac{{2(AD - BD)}}{\lambda } < 2k + 1 < \dfrac{{2AB}}{\lambda }\). Thay số :
\(\dfrac{{2(20 - 20\sqrt 2 )}}{{1,5}} < 2k + 1 < \dfrac{{2.20}}{{1,5}}\) =>\( - 11,04 < 2k + 1 < 26,67\) Vậy: -6,02<k<12,83. Có $19$ điểm cực đại
Trên mặt thoáng của chất lỏng có hai nguồn kết hợp A và B giống nhau dao động cùng tần số \(f = 8Hz\) tạo ra hai sóng lan truyền với \(v = 16cm/s\). Hai điểm MN nằm trên đường nối \(AB\), nằm ở hai phía của trung điểm O của đoạn AB và cách trung điểm O của AB các đoạn lần lượt là \(OM = 3,75 cm\), \(ON = 2,25cm\). Số điểm dao động với biên độ cực đại và cực tiểu trong đoạn MN là:
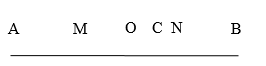
Giả sử biểu thức sóng của hai nguồn \({u_1} = {\rm{ }}{u_2} = acos\omega t\)
Bước sóng: \(\lambda = \dfrac{v}{f} = \dfrac{{16}}{8} = 2cm\), O là trung điểm của AB
Xét điểm C trên MN: \(OC=d\) \((0 < d < \dfrac{{AB}}{2})\)
\(\left\{ \begin{array}{l}{u_{1M}} = ac{\rm{os(}}\omega t - \dfrac{{2\pi \left( {\dfrac{{AB}}{2} + d} \right)}}{\lambda }) = ac{\rm{os}}\left( {\omega t - \pi d - \dfrac{{AB}}{2}\pi } \right)\\{u_{2M}} = ac{\rm{os(}}\omega t - \dfrac{{2\pi \left( {\dfrac{{AB}}{2} - d} \right)}}{\lambda }) = ac{\rm{os}}\left( {\omega t + \pi d - \dfrac{{AB}}{2}\pi } \right)\end{array} \right.\)
+ Điểm M dao động với biên độ cực đại khi \({u_{{S_1}M}}\) và \({u_{{S_2}M}}\) cùng pha với nhau
\(2\pi d = 2k\pi \Rightarrow d = k\)
Với :
\(\begin{array}{l} - 3,75 \le d \le 2,25\\ \Rightarrow - 3,75 \le k \le 2,25\\ \Rightarrow k = - 3, \pm 2, \pm 1,0\end{array}\)
=> Có 6 cực đại
+ Điểm M dao động với biên độ cực đại khi \({u_{{S_1}M}}\) và \({u_{{S_2}M}}\) ngược pha với nhau
\(\begin{array}{l}2\pi d = \left( {2k + 1} \right)\pi \\ \Rightarrow d = \dfrac{{2k + 1}}{2} = k + \dfrac{1}{2}\end{array}\)
Với
\(\begin{array}{l} - 3,75 \le d \le 2,25\\ \Rightarrow - 3,75 \le k + \dfrac{1}{2} \le 2,25\\ \Leftrightarrow - 4,25 \le k + \dfrac{1}{2} \le 1,75\\ \Rightarrow k = - 4, - 3, - 2, \pm 1,0\end{array}\)
=> Có 6 cực tiểu .
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 24 cm, dao động theo phương thẳng đứng với phương trình là uA=uB=acos60πt (với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là v=45cm/s. Gọi MN=4cm là đoạn thẳng trên mặt chất lỏng có chung trung trực với AB. Khoảng cách xa nhất giữa MN với AB là bao nhiêu để có ít nhất 5 điểm dao động cực đại nằm trên MN?
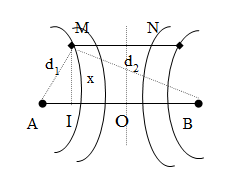
Bước sóng \(\lambda = \dfrac{v}{f} = \dfrac{{45}}{{30}} = 1,5cm\)
Muốn trên MN có ít nhất 5 điểm dao động với biên độ cực đại thì M và N phải thuộc đường cực đại thứ 2 tính từ cực đại trung tâm.
Xét M ta có \({d_2} - {d_1} = 2\lambda = 2.1,5 = 3cm\) (1) (cực đại thứ 2 nên k=2)
Ta có : \(OA = OB = \dfrac{{AB}}{2} = \dfrac{{24}}{2} = 12cm\)
\(OI = \dfrac{{MN}}{2} = \dfrac{4}{2} = 2cm\)
\( \Rightarrow \left\{ \begin{array}{l}BI = OB + OI = 12 + 2 = 14cm\\AI = AB - BI = 24 - 14 = 10cm\end{array} \right.\)
Suy ra : \(\left\{ \begin{array}{l}{d_2} = \sqrt {M{I^2} + B{I^2}} = \sqrt {{x^2} + {{14}^2}} \\{d_1} = \sqrt {M{I^2} + A{I^2}} = \sqrt {{x^2} + {{10}^2}} \end{array} \right.\)
Thay vào (1), ta được :
\(\begin{array}{l}\sqrt {{x^2} + {{14}^2}} - \sqrt {{x^2} + {{10}^2}} = 3\\ \Rightarrow x = 10,5cm\end{array}\)
Hai nguồn sóng kết hợp giống hệt nhau được đặt cách nhau một khoảng cách x trên đường kính của một vòng tròn bán kính \(R\) \((x << R)\) và đối xứng qua tâm của vòng tròn. Biết rằng mỗi nguồn đều phát sóng có bước sóng \(λ\) và \(x = 6λ\). Số điểm dao động cực đại trên vòng tròn là:
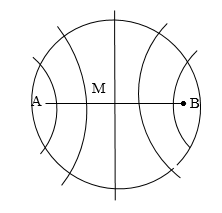
Cách 1: Xét điểm M trên AB (AB = 2x = 12l) AM = d1; BM = d2
d1 – d2 = kλ; d1 + d2 = 6λ;
=> d1 = (3 + 0,5k)λ
0 ≤ d1 = (3 + 0,5k)λ ≤ 6λ
=> - 6 ≤ k ≤ 6
Số điểm dao động cực đại trên AB là 13 điểm kể cả hai nguồn A, B.
Nhưng số đường cực đại cắt đường tròn chỉ có 11 vì vậy, số điểm dao động cực đại trên vòng tròn là 22.
Cách 2: Các vân cực đại gồm các đường hyperbol nhận 2 nguồn làm tiêu điểm nên tại vị trí nguồn không có các hyperbol do đó khi giải bài toán này ta chỉ có
\( - 6\lambda < k\lambda < 6\lambda \)
( không có dấu bằng) nên chỉ có 11 vân cực đại do đó cắt đường tròn 22 điểm cực đại .
Trên bề mặt chất lỏng có hai nguồn kết hợp $AB$ cách nhau $40cm$ dao động cùng pha. Biết sóng do mỗi nguồn phát ra có tần số $f=10(Hz)$, vận tốc truyền sóng $2(m/s)$. Gọi $M$ là một điểm nằm trên đường vuông góc với $AB$ tại $A$ và dao đông với biên độ cực đại. Đoạn $AM$ có giá trị lớn nhất là :
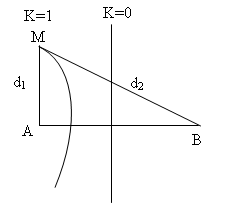
Ta có
\(\lambda = \dfrac{v}{f} = \dfrac{{200}}{{10}} = 20(cm)\).
Do M là một cực đại giao thoa nên để đoạn AM có giá trị lớn nhất thì M phải nằm trên vân cực đại bậc 1 như hình vẽ và thõa mãn:
\({d_2} - {d_1} = k\lambda = 1.20 = 20(cm)\) (1). ( do lấy k = +1)
Mặt khác, do tam giác AMB là tam giác vuông tại A nên ta có :
\(BM = {d_2} = \sqrt {(A{B^2}) + (A{M^2})} = \sqrt {{{40}^2} + {d_1}^2} (2)\)
Thay (2) vào (1) ta được :
\(\sqrt {{{40}^2} + {d_1}^2} - {d_1} = 20 \Rightarrow {d_1} = 30(cm)\)
Trên bề mặt chất lỏng có hai nguồn kết hợp \(AB\) cách nhau \(100cm\) dao động cùng pha. Biết sóng do mỗi nguồn phát ra có tần số \(f=10(Hz)\), vận tốc truyền sóng \(3(m/s)\). Gọi \(M\) là một điểm nằm trên đường vuông góc với \(AB\) tại đó \(M\) dao đông với biên độ cực đại. Đoạn \(AM\) có giá trị nhỏ nhất là :
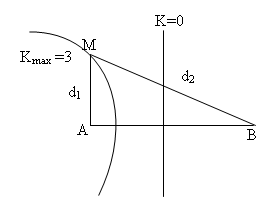
Ta có
\(\lambda = \dfrac{v}{f} = \dfrac{{300}}{{10}} = 30(cm)\).
Số vân dao động với biên độ dao động cực đại trên đoạn AB thõa mãn điều kiện :
\( - AB < {d_2} - {d_1} = k\lambda < AB\).
Hay :
\(\dfrac{{ - AB}}{\lambda } < k < \dfrac{{AB}}{\lambda } \Leftrightarrow \dfrac{{ - 100}}{3} < k < \dfrac{{100}}{3} \Leftrightarrow - 3,3 < k < 3,3\). =>\(k = 0, \pm 1, \pm 2, \pm 3\).
=>Đoạn AM có giá trị bé nhất thì M phải nằm trên đường cực đại bậc 3 (kmax) như hình vẽ và thõa mãn : \({d_2} - {d_1} = k\lambda = 3.30 = 90(cm)\)
(1) ( do lấy k=3) Mặt khác, do tam giác AMB là tam giác vuông tại A nên ta có :
\(BM = {d_2} = \sqrt {(A{B^2}) + (A{M^2})} = \sqrt {{{100}^2} + {d_1}^2} (2)\)
Thay (2) vào (1) ta được :
\(\sqrt {{{100}^2} + {d_1}^2} - {d_1} = 90 \Rightarrow {d_1} = 10,56(cm)\)
Giao thoa sóng nước với hai nguồn giống hệt nhau A, B cách nhau 20cm có tần số 50Hz. Tốc độ truyền sóng trên mặt nước là 1,5m/s. Trên mặt nước xét đường tròn tâm A, bán kính AB. Điểm trên đường tròn dao động với biên độ cực đại cách đường thẳng qua A, B một đoạn gần nhất là:

\( = > h = \sqrt {d_2^2 - {x^2}} = \sqrt {{{20}^2} - 1} = \sqrt {399} = 19,97mm\)
Hai nguồn sóng $AB$ cách nhau $1 m$ dao động cùng pha với bước sóng $0,5m$. $I$ là trung điểm $AB$. $H$ là điểm nằm trên đường trung trực của $AB$ cách $I$ một đoạn $1,5m$. Gọi $d$ là đường thẳng qua $H$ và song song với $AB$. Tìm điểm $M$ thuộc $d$ và gần $H$ nhất, dao động với biên độ cực đại. (Tìm khoảng cách $MH$)
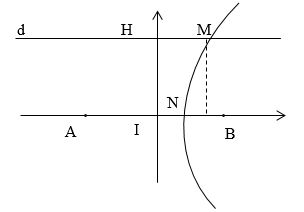
Cách 1:
Vì A và B cùng pha, do đó I dao động với biên độ cực đại.
Gọi N là giao của đường cực đại qua M và đường AB.
Vì M gần H nhất và dao động với biên độ cực đại nên
\(NI = \dfrac{\lambda }{2} = 0,25m\)
Theo tính chất về đường Hypecbol ta có:
Khoảng cách $BI{\rm{ }} = {\rm{ }}c{\rm{ }} = {\rm{ }}0,5m$
Khoảng cách $IN{\rm{ }} = {\rm{ }}a{\rm{ }} = {\rm{ }}0,25m$
Mà ta có ${b^2} + {a^2} = {c^2}$ . Suy ra ${b^2} = {a^2} - {c^2} = 0,{5^2} - 0,{25^2} = 0,1875$
Toạ độ điểm M là x, y thoả mãn: $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$
Với $x{\rm{ }} = {\rm{ }}MH,{\rm{ }}y{\rm{ }} = {\rm{ }}HI{\rm{ }} = 1,5m$
$\dfrac{{M{H^2}}}{{0,{{25}^2}}} - \dfrac{{1,{5^2}}}{{0,1875}} = 1 \to MH = 0,9m$
Cách 2:
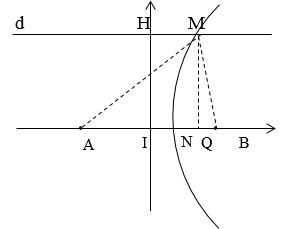
Vì A và B cùng Hha và M gần H nhất và dao động với
biên độ cực đại nên M thuộc cực đại ứng với $k{\rm{ }} = 1$
Ta có: \(MA - MB = k\lambda = \lambda \)
Theo hình vẽ ta có: $\sqrt {A{Q^2} + M{Q^2}} - \sqrt {B{Q^2} + M{Q^2}} = \lambda $
Đặt $MH{\rm{ }} = {\rm{ }}IQ{\rm{ }} = {\rm{ }}x$ , có $HI{\rm{ }} = {\rm{ }}MQ{\rm{ }} = 1,5m$
Ta có:
$\begin{array}{l}\sqrt {{{(0,5 + x)}^2} + 1,{5^2}} - \sqrt {{{(0,5 - x)}^2} + 1,{5^2}} = 0,5\\ \to x = 0,9m\end{array}$
Ở mặt nước, tại hai điểm A và B cách nhau \(19 cm\), có hai nguồn kết hợp dao động cùng pha theo phương thẳng đứng, phát ra hai sóng có bước sóng \(4 cm\). Trong vùng giao thoa, M là một điểm ở mặt nước thuộc đường trung trực của AB. Trên đoạn AM, số điểm cực tiểu giao thoa là
Số điểm dao động với biên độ cực tiểu trên đoạn AM bằng số giá trị k thỏa mãn điều kiện
\(\begin{array}{l}BM - AM \le {d_2} - {d_1} < AB \Leftrightarrow 0 \le \left( {k + \dfrac{1}{2}} \right)4 < 19\\ - 0,5 < k < 4,25 = > k = 0;1;2;3;4\end{array}\)
Có 5 giá trị k thỏa mãn điều kiện.
Hai nguồn kết hợp A, B cách nhau \(16cm\) đang cùng dao động vuông góc với mặt nước theo phương trình \(u = acos50\pi t\left( {cm} \right)\). Xét một điểm C trên mặt nước thuộc cực tiểu giao thoa, giữa C và trung trực của AB có một đường cực đại giao thoa. Biết \(AC = 17,2cm\); \(BC = 13,6cm\). Số điểm cực đại trên đoạn thẳng \(AC\) là
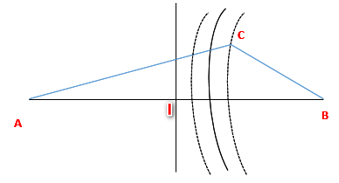
Ta có, giữa C và trung trực AB có một đường cực đại giao thoa
\( \Rightarrow C\) là cực tiểu bậc 2
\(\begin{array}{l}CA - CB = 1,5\lambda \\ \Leftrightarrow 17,2 - 13,6 = 1,5\lambda \\ \Rightarrow \lambda = 2,4cm\end{array}\)
Số điểm cực đại trên AC là:
\({d_{1A}} - {d_{2A}} \le k\lambda \le {d_{1C}} - {d_{2C}}\)
\( \Leftrightarrow 0 - 16 \le k.2,4 \le 17,2 - 13,6\)
\( \Leftrightarrow - 6,6 \le k \le 1,5\)
Suy ra có 8 điểm cực đại trên đoạn thẳng AC
Ở mặt chất lỏng, tại hai điểm \({S_1}\) và \({S_2}\) cách nhau 28 cm có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra sóng kết hợp. Gọi \({\Delta _1}\) và \({\Delta _2}\) là hai đường thẳng ở mặt chất lỏng cùng vuông góc với đoạn thẳng \({S_1}\) \({S_2}\) và cách nhau 9 cm. Biết số điểm cục đại giao thoa trên \({\Delta _1}\)và \({\Delta _2}\) tương ứng là 7 và 3. Số điểm cực đại giao thoa trên đoạn thẳng \({S_1}{S_2}\) là
Ta có hình vẽ:
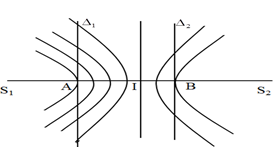
Từ hình vẽ ta thấy, để trên \({\Delta _1}\) có 7 cực đại, tại điểm A là cực đại bậc 4 \( \Rightarrow IA = 4\dfrac{\lambda }{2} = 2\lambda \)
Trên \({\Delta _2}\) có 3 cực đại, tại điểm B là cực đại bậc 2 \( \Rightarrow IB = 2\dfrac{\lambda }{2} = \lambda \)
Khoảng cách giữa \({\Delta _1}\) và \({\Delta _2}\) là:
\(AB = 3\lambda = 9\left( {cm} \right) \Rightarrow \lambda = 3\left( {cm} \right)\)
Số điểm cực đại trên đoạn \({S_1}{S_2}\) là: \(n = 2\left[ {\dfrac{{{S_1}{S_2}}}{\lambda }} \right] + 1 = 2.\left[ {\dfrac{{28}}{3}} \right] + 1 = 19\) (cực đại)

