Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 24 cm, dao động theo phương thẳng đứng với phương trình là uA=uB=acos60πt (với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là v=45cm/s. Gọi MN=4cm là đoạn thẳng trên mặt chất lỏng có chung trung trực với AB. Khoảng cách xa nhất giữa MN với AB là bao nhiêu để có ít nhất 5 điểm dao động cực đại nằm trên MN?
Trả lời bởi giáo viên
Bước sóng \(\lambda = \dfrac{v}{f} = \dfrac{{45}}{{30}} = 1,5cm\)
Muốn trên MN có ít nhất 5 điểm dao động với biên độ cực đại thì M và N phải thuộc đường cực đại thứ 2 tính từ cực đại trung tâm.
Xét M ta có \({d_2} - {d_1} = 2\lambda = 2.1,5 = 3cm\) (1) (cực đại thứ 2 nên k=2)
Ta có : \(OA = OB = \dfrac{{AB}}{2} = \dfrac{{24}}{2} = 12cm\)
\(OI = \dfrac{{MN}}{2} = \dfrac{4}{2} = 2cm\)
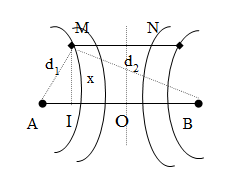
\( \Rightarrow \left\{ \begin{array}{l}BI = OB + OI = 12 + 2 = 14cm\\AI = AB - BI = 24 - 14 = 10cm\end{array} \right.\)
Suy ra : \(\left\{ \begin{array}{l}{d_2} = \sqrt {M{I^2} + B{I^2}} = \sqrt {{x^2} + {{14}^2}} \\{d_1} = \sqrt {M{I^2} + A{I^2}} = \sqrt {{x^2} + {{10}^2}} \end{array} \right.\)
Thay vào (1), ta được :
\(\begin{array}{l}\sqrt {{x^2} + {{14}^2}} - \sqrt {{x^2} + {{10}^2}} = 3\\ \Rightarrow x = 10,5cm\end{array}\)
Hướng dẫn giải:
+ Áp dụng biểu thức xác định bước sóng: \(\lambda = \dfrac{v}{f}\)
+ Áp dụng điều kiện dao động cực đại của 2 nguồn cùng pha: d2 - d1 = kλ

