Trên bề mặt chất lỏng có đặt hai nguồn kết hợp A, B cách nhau 46,25cm và dao động cùng pha. Sóng do mỗi nguồn phát ra có tần số f=40Hz, vận tốc truyền sóng là 5m/s. Trên mặt chất lỏng, gọi M là một điểm nằm trên đường thẳng vuông góc với AB tại A và dao động với biên độ cực tiểu. Đoạn BM có giá trị cực đại là
Ta có:
+ Bước sóng: \(\lambda = \dfrac{v}{f} = \dfrac{5}{{40}} = 0,125m = 12,5cm\)
M dao động với biên độ cực tiểu \( \Rightarrow AM - BM = \left( {2k + 1} \right)\dfrac{\lambda }{2}\)
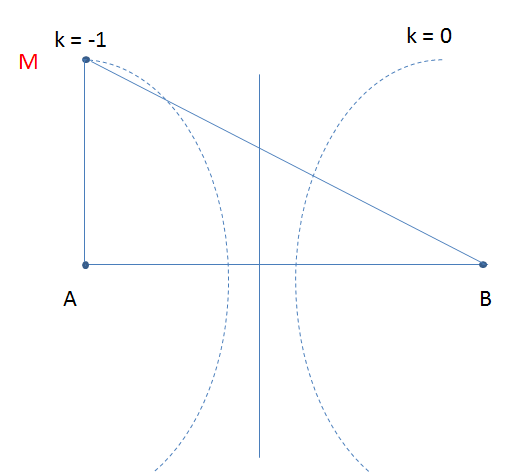
Để đoạn \(BM\) cực đại \( \Rightarrow M\) là cực tiểu ứng với \(k = - 1\)
\( \Rightarrow AM - BM = - \dfrac{\lambda }{2}\)
\(\begin{array}{l} \Leftrightarrow \sqrt {B{M^2} - A{B^2}} - BM = - \dfrac{\lambda }{2}\\ \Rightarrow \sqrt {B{M^2} - A{B^2}} = BM - \dfrac{\lambda }{2}\\ \Rightarrow \left\{ \begin{array}{l}BM \ge \dfrac{\lambda }{2}\\B{M^2} - A{B^2} = B{M^2} - BM\lambda + \dfrac{{{\lambda ^2}}}{4}\end{array} \right.\\ \Rightarrow BM = \dfrac{{A{B^2} + \dfrac{{{\lambda ^2}}}{4}}}{\lambda } = \dfrac{{46,{{25}^2} + \dfrac{{12,{5^2}}}{4}}}{{12,5}} = 174,25cm\end{array}\)
Trên mặt nước, hai nguồn kết hợp A, B cách nhau 40cm luôn dao động cùng pha, có bước sóng 6cm. Hai điểm CD nằm trên mặt nước mà ABCD là một hình chữ nhật, AD = 30cm. Số điểm cực đại và đứng yên trên đoạn CD lần lượt là
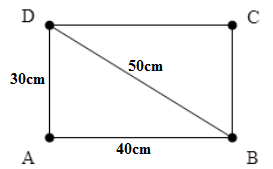
Áp dụng định lí Pitago ta có: \(DB = CA = 50cm\)
+ Số điểm cực đại giao thoa trên đoạn CD bằng số giá trị k nguyên thoả mãn:
\(\begin{array}{l}\dfrac{{CB - CA}}{\lambda } \le k \le \dfrac{{DB - DA}}{\lambda } \Leftrightarrow \dfrac{{30 - 50}}{6} \le k \le \dfrac{{50 - 30}}{6}\\ \Leftrightarrow - 3,3 \le k \le 3,3 \Rightarrow k = - 3; - 2;...;3\end{array}\)
Có 7 giá trị của k nguyên thoả mãn nên có 7 cực đại giao thoa
+ Số điểm đứng yên trên đoạn CD bằng số giá trị k nguyên thoả mãn:
\(\begin{array}{l}\dfrac{{CB - CA}}{\lambda } - \dfrac{1}{2} \le k \le \dfrac{{DB - DA}}{\lambda } - \dfrac{1}{2}\\ \Leftrightarrow \dfrac{{30 - 50}}{6} - \dfrac{1}{2} \le k \le \dfrac{{50 - 30}}{6} - \dfrac{1}{2}\\ \Leftrightarrow - 3,8 \le k \le 2,8 \Rightarrow k = - 3; - 2;...;2\end{array}\)
Có 6 giá trị của k nguyên thoả mãn nên có 6 điểm đứng yên.
Trong thí nghiệm giao thoa sóng nước với hai nguồn kết hợp cùng pha và cùng biên độ, cùng bước sóng λ. Người ta thấy phần tử nước tại điểm M không dao động. Hiệu khoảng cách từ M đến hai nguồn có thể nhận giá trị nào sau đây?
Điểm M không dao động là điểm cực tiểu, có:
\({d_2} - {d_1} = \left( {k + \dfrac{1}{2}} \right)\lambda = \dfrac{\lambda }{2}\)
Trong thí nghiệm giao thoa sóng nước, hai nguồn kết hợp A và B dao động cùng pha với tần số \(20 Hz.\) Người ta thấy điểm M dao động cực đại và giữa M với đường trung trực của AB có một đường không dao động. Điểm M thuộc cực đại ứng với
Ta có hình ảnh giao thoa sóng:
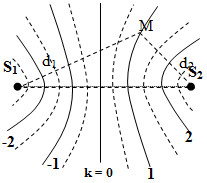
Giữa \(M\) và đường trung trực của \(AB\) có một đường không dao động
\( \Rightarrow \) Điểm \(M\) thuộc cực đại ứng với \(k = 1.\)
Đề thi THPT QG - 2020
Thí nghiệm giao thoa sóng ở mặt chất lỏng với hai nguồn kết hợp đặt tại A và B cách nhau 10,6 cm dao động cùng pha theo phương thẳng đứng. Trên đoạn thẳng AB, khoảng cách từ A tới cực đại giao thoa xa A nhất là 10,0 cm. Biết số vân giao thoa cực đại nhiều hơn số vân giao thoa cực tiểu. Số vân giao thoa cực đại nhiều nhất là
Gọi C là vị trí cực đại xa A nhất.
Từ hình ta có: \(d + \frac{\lambda }{4} > AB \Rightarrow \lambda > 4\left( {AB - d} \right) = 2,4cm\) (1) \( \Rightarrow \frac{{AB}}{\lambda } < \frac{{AB}}{{2,4}} = 4,42\)
+ Xét trường hợp có 4 cực đại ở mỗi bên của đường trung trực của AB.
Điểm C phải thỏa mãn: \(CA - CB = 4\lambda \)
\( \Rightarrow \lambda = \frac{{CA - CB}}{4} = \frac{{CA - \left( {AB - CA} \right)}}{4} = \frac{{2CA - AB}}{4} = 2,35cm\) trái với (1)\( \Rightarrow \) Loại
+ Xét trường hợp có 3 cực đại ở mỗi bên của trung trực của AB.
Điểm C phải thỏa mãn: \(CA - CB = 3\lambda \)
\( \Rightarrow \lambda = \frac{{CA - CB}}{3} = \frac{{CA - \left( {AB - CA} \right)}}{3} = \frac{{2CA - AB}}{3} = 3,13cm\) thỏa mãn (1)
\( \Rightarrow \) Vậy có 7 cực đại tối đa trên AB
Đề thi thử THPT chuyên Lam Sơn - 2021
Ở mặt chất lỏng, tại hai điểm A và B có hai nguồn dao động cùng pha theo phương vuông góc với mặt chất lỏng phát ra hai sóng kết hợp với bước sóng \(\lambda \). Gọi C, D là hai điểm ở mặt chất lỏng sao cho ABCD là hình vuông. I là trung điểm của AB. M là một điểm nằm trong hình vuông ABCD xa I nhất mà phần tử chất lỏng tại đó dao động với biên độ cực đại và cùng pha với nguồn. Biết \(AB = 2,4\lambda \). Độ dài đoạn thẳng MI gần nhất giá trị nào sau đây?
Chuẩn hóa, ta cho \(\lambda = 1 \Rightarrow \left\{ \begin{array}{l}AB = 2,4\\AC = AB\sqrt 2 = 2,4\sqrt 2 \end{array} \right.\)
M dao động với biên độ cực đại, cùng pha với nguồn:
\(\left\{ \begin{array}{l}MA = {k_1}\lambda = {k_1}\\MB = {k_2}\lambda = {k_2}\end{array} \right.\) với \({k_1},{k_2}\) là số nguyên.
Ta có:
*\(CI\) là trung tuyến của \(\Delta CAB\) nên ta có: \(C{I^2} = \frac{{A{C^2} + B{C^2}}}{2} - \frac{{A{B^2}}}{4}\)
\( \Rightarrow CI = \sqrt {\frac{{{{\left( {2,4\sqrt 2 } \right)}^2} + 2,{4^2}}}{2} - \frac{{2,{4^2}}}{4}} = \frac{{6\sqrt 5 }}{5}\)
* MI là trung tuyến của \(\Delta MAB\) nên ta có: \(M{I^2} = \frac{{M{A^2} + M{B^2}}}{2} - \frac{{A{B^2}}}{4}\)
Lại có M là 1 điểm nằm trong hình vuông ABCD nên:
+ \(MA < AC \Leftrightarrow {k_1} < 2,4\sqrt 2 = 3,39 \Rightarrow {k_1} \le 3\)
+ \(MI < CI \Leftrightarrow \frac{{M{A^2} + M{B^2}}}{2} - \frac{{A{B^2}}}{4} < B{C^2} + B{I^2}\)
\(\begin{array}{l} \Leftrightarrow \frac{{M{A^2} + M{B^2}}}{2} - \frac{{A{B^2}}}{4} < A{B^2} + \frac{{A{B^2}}}{4}\\ \Rightarrow \frac{{M{A^2} + M{B^2}}}{2} < \frac{3}{2}A{B^2} = \frac{3}{2}.2,{4^2} = 8,64\end{array}\)
\( \Rightarrow M{A^2} + M{B^2} < 17,28 \Rightarrow k_1^2 + k_2^2 < 17,28\,\,\,\,\left( 1 \right)\)
Lại có: \(M{B^2} + A{B^2} > M{A^2} \Rightarrow k_2^2 + 2,{4^2} > k_1^2\,\,\,\left( 2 \right)\)
Đặt \(MH = x\) \(\left( {x < 2,4} \right)\)\( \Rightarrow \sqrt {M{A^2} - {x^2}} + \sqrt {M{B^2} - {x^2}} = AB\)
\( \Rightarrow \sqrt {k_1^2 - {x^2}} + \sqrt {k_2^2 - {x^2}} = 2,4\,\,\,\,\,\left( 3 \right)\)
Xét các cặp \({k_1}\) và \({k_2}\) thỏa mãn (1), (2) và (3) ta tìm được \(\left\{ \begin{array}{l}{k_1} = 3\\{k_2} = 2\end{array} \right.\) \(\)
\( \Rightarrow MI = \sqrt {\frac{{k_1^2 + k_2^2}}{2} - \frac{{2,{4^2}}}{4}} = 2,2494\)
Hai nguồn phát sóng kết hợp tại A, B trên mặt nước cách nhau 12cm phát ra hai dao động điều hòa cùng tần số 20Hz, cùng biên độ và cùng pha ban đầu. Xét điểm M trên mặt nước cách A, B những đoạn lần lượt là 4,2cm và 9cm. Tốc độ truyền sóng trên mặt nước là 32cm/s. Muốn M là một điểm dao động với biên độ cực tiểu thì phải dịch chuyển nguồn tại B dọc đường nối A, B từ vị trí ban đầu ra xa nguồn A một đoạn nhỏ nhất là:
Bước sóng: \(\lambda = \dfrac{v}{f} = \dfrac{{32}}{{20}} = 1,6cm\)
Xét tỉ số: \(\dfrac{{{d_2} - {d_1}}}{\lambda } = \dfrac{{9 - 4,2}}{{1,6}} = 3\)
Vậy ban đầu M nằm trên cực đại bậc 3.
Dịch chuyển B ra xa một đoạn ∆d, để đoạn này là nhỏ nhất thì khi đó M phải nằm trên cực tiểu thứ 4 với:
\({d_2}' - {d_1} = \left( {3 + \dfrac{1}{2}} \right)\lambda = 3,5\lambda = 3,5.1,6 = 5,6cm \Rightarrow {d_2}' = 9,8cm\)
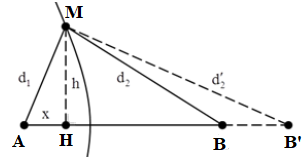
Áp dụng đinh lí hàm số cos cho tam giác MAB ta có:
\(\begin{array}{l}M{B^2} = M{A^2} + A{B^2} - 2.AM.AB.cosA\\ \Rightarrow cosA = \dfrac{{M{A^2} + A{B^2} - M{B^2}}}{{2.AM.AB}} = \dfrac{{4,{2^2} + {{12}^2} - {9^2}}}{{2.4,2.12}} = 0,8\end{array}\)
\( \Rightarrow \left\{ \begin{array}{l}AH = AM.\cos A = 4,2.0,8 = 3,36cm\\MH = AM.sinA = 4,2.0,6 = 2,52cm\end{array} \right.\)
Áp dụng định lí Pitago trong tam giác vuông MHB’ ta có:
\(HB' = \sqrt {MB{'^2} - M{H^2}} = \sqrt {9,{8^2} - 2,{{52}^2}} = 9,47cm\)
Đoạn dịch chuyển:
\(\begin{array}{l}BB' = HB' - HB = HB' - \left( {AB - AH} \right)\\ \Rightarrow BB' = 9,47 - \left( {12 - 3,36} \right) = 0,83cm\end{array}\)

