Trên bề mặt chất lỏng có đặt hai nguồn kết hợp A, B cách nhau 46,25cm và dao động cùng pha. Sóng do mỗi nguồn phát ra có tần số f=40Hz, vận tốc truyền sóng là 5m/s. Trên mặt chất lỏng, gọi M là một điểm nằm trên đường thẳng vuông góc với AB tại A và dao động với biên độ cực tiểu. Đoạn BM có giá trị cực đại là
Trả lời bởi giáo viên
Ta có:
+ Bước sóng: \(\lambda = \dfrac{v}{f} = \dfrac{5}{{40}} = 0,125m = 12,5cm\)
M dao động với biên độ cực tiểu \( \Rightarrow AM - BM = \left( {2k + 1} \right)\dfrac{\lambda }{2}\)
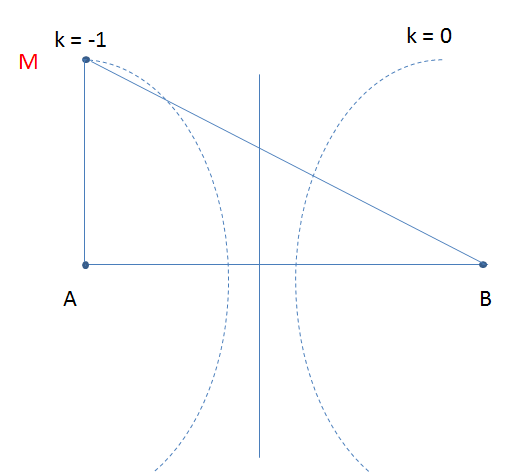
Để đoạn \(BM\) cực đại \( \Rightarrow M\) là cực tiểu ứng với \(k = - 1\)
\( \Rightarrow AM - BM = - \dfrac{\lambda }{2}\)
\(\begin{array}{l} \Leftrightarrow \sqrt {B{M^2} - A{B^2}} - BM = - \dfrac{\lambda }{2}\\ \Rightarrow \sqrt {B{M^2} - A{B^2}} = BM - \dfrac{\lambda }{2}\\ \Rightarrow \left\{ \begin{array}{l}BM \ge \dfrac{\lambda }{2}\\B{M^2} - A{B^2} = B{M^2} - BM\lambda + \dfrac{{{\lambda ^2}}}{4}\end{array} \right.\\ \Rightarrow BM = \dfrac{{A{B^2} + \dfrac{{{\lambda ^2}}}{4}}}{\lambda } = \dfrac{{46,{{25}^2} + \dfrac{{12,{5^2}}}{4}}}{{12,5}} = 174,25cm\end{array}\)
Hướng dẫn giải:
+ Sử dụng biểu thức: \(\lambda = \dfrac{v}{f}\)
+ Sử dụng điều kiện cực tiểu dao động: \({d_2} - {d_1} = \left( {2k + 1} \right)\dfrac{\lambda }{2}\)

