Trên mặt nước, hai nguồn kết hợp A, B cách nhau 40cm luôn dao động cùng pha, có bước sóng 6cm. Hai điểm CD nằm trên mặt nước mà ABCD là một hình chữ nhật, AD = 30cm. Số điểm cực đại và đứng yên trên đoạn CD lần lượt là
Trả lời bởi giáo viên
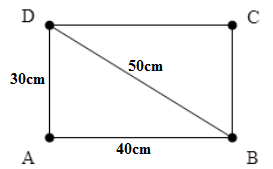
Áp dụng định lí Pitago ta có: \(DB = CA = 50cm\)
+ Số điểm cực đại giao thoa trên đoạn CD bằng số giá trị k nguyên thoả mãn:
\(\begin{array}{l}\dfrac{{CB - CA}}{\lambda } \le k \le \dfrac{{DB - DA}}{\lambda } \Leftrightarrow \dfrac{{30 - 50}}{6} \le k \le \dfrac{{50 - 30}}{6}\\ \Leftrightarrow - 3,3 \le k \le 3,3 \Rightarrow k = - 3; - 2;...;3\end{array}\)
Có 7 giá trị của k nguyên thoả mãn nên có 7 cực đại giao thoa
+ Số điểm đứng yên trên đoạn CD bằng số giá trị k nguyên thoả mãn:
\(\begin{array}{l}\dfrac{{CB - CA}}{\lambda } - \dfrac{1}{2} \le k \le \dfrac{{DB - DA}}{\lambda } - \dfrac{1}{2}\\ \Leftrightarrow \dfrac{{30 - 50}}{6} - \dfrac{1}{2} \le k \le \dfrac{{50 - 30}}{6} - \dfrac{1}{2}\\ \Leftrightarrow - 3,8 \le k \le 2,8 \Rightarrow k = - 3; - 2;...;2\end{array}\)
Có 6 giá trị của k nguyên thoả mãn nên có 6 điểm đứng yên.
Hướng dẫn giải:
Số điểm cực đại giao thoa trên đoạn CD bằng số giá trị k nguyên thoả mãn:
\(\dfrac{{\Delta {d_C}}}{\lambda } \le k \le \dfrac{{\Delta {d_D}}}{\lambda }\)
Số điểm đứng yên trên đoạn CD bằng số giá trị k nguyên thoả mãn:
\(\dfrac{{\Delta {d_C}}}{\lambda } - \dfrac{1}{2} \le k \le \dfrac{{\Delta {d_D}}}{\lambda } - \dfrac{1}{2}\)

