Hai nguồn kết hợp A, B cách nhau \(16cm\) đang cùng dao động vuông góc với mặt nước theo phương trình \(u = acos50\pi t\left( {cm} \right)\). Xét một điểm C trên mặt nước thuộc cực tiểu giao thoa, giữa C và trung trực của AB có một đường cực đại giao thoa. Biết \(AC = 17,2cm\); \(BC = 13,6cm\). Số điểm cực đại trên đoạn thẳng \(AC\) là

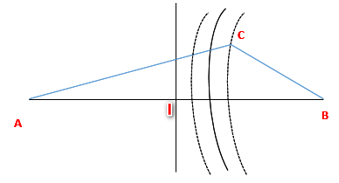
Tại hai điểm A, B cách nhau 14cm thuộc bề mặt chất lỏng người ta đặt hai nguồn sóng kết hợp dao động theo phương thẳng đứng với phương trình \({u_A} = {u_B} = Acos\left( {\omega t} \right)\left( {cm} \right)\). Điểm N thuộc mặt thoáng  chất lỏng cách nguồn A, B lần lượt 8cm và 17cm có biên độ sóng cực đại. Giữa N và đường trung trực của AB có hai dãy cực đại khác. Xem quá trình lan truyền sóng biên độ không đổi, không tiêu hao năng lượng. Tại mặt thoáng chất lỏng, xét điểm M thuộc đường tròn tâm B bán kính AB cũng có biên độ sóng cực đại và xa điểm A nhất. Khoảng cách từ điểm B đến hình chiếu của điểm M xuống đường thẳng nối AB là

Đề thi THPT QG - 2020

Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp dao động cùng pha theo phương thẳng đứng phát ra hai sóng có bước sóng \(\lambda \). Cực đại giao thoa tại các điểm có hiệu đường đi của hai sóng từ nguồn truyền tới đó bằng

Ở mặt nước, tại hai điểm A và B cách nhau \(8cm\) có hai nguồn giống nhau dao động theo phương thẳng đứng, phát ra hai sóng có bước sóng \(1cm\). M, N là hai điểm thuộc mặt nước cách nhau \(4cm\) và ABMN là hình thang cân (AB // MN). Để trong đoạn MN có đúng \(5\) điểm dao động với biên độ cực đại thì diện tích lớn nhất của hình thang có giá trị nào sau đây?

Trên mặt nước có hai nguồn sóng nước giống nhau cách nhau \(AB = 12\left( {cm} \right)\). Sóng truyền trên mặt nước có bước sóng \(1,6\left( {cm} \right)\). Số đường cực đại đi qua đoạn thẳng nối hai nguồn là:

Hai nguồn kết hợp A, B cách nhau \(32mm\) ở trên mặt thoáng chất lỏng dao động theo phương trình \({u_1} = {u_2} = 2cos100\pi t{\rm{ }}\left( {mm} \right)\). Trên mặt thoáng chất lỏng có hai điểm M và M’ ở cùng một phía của đường trung trực của AB thỏa mãn: \(MA - MB = 12mm\) và \(M'A{\rm{ }} - {\rm{ }}M'B = 28mm\). Hai điểm đó đều nằm trên các vân giao thoa cùng loại và giữa chúng chỉ có một vân loại đó. Vận tốc truyền sóng trên mặt chất lỏng là:

Tại hai điểm A, B trên mặt chất lỏng cách nhau \(12cm\) có hai nguồn phát sóng theo phương thẳng đứng với các phương trình : \({u_1} = 0,2.cos(50\pi t)cm\) và\({u_2} = 0,2.cos(50\pi t + \pi )cm\). Vận tốc truyền sóng là \(0,5{\rm{ }}\left( {m/s} \right)\). Coi biên độ sóng không đổi. Xác định số điểm dao động với biên độ cực đại trên đoạn thẳng AB ?