Ở mặt thoáng của một chất lỏng có hai nguồn kết hợp $A$ và $B$ cách nhau $20(cm)$ dao động theo phương thẳng đứng với phương trình \({u_A} = 2.cos(40\pi t)(mm)\) và \({u_B} = 2.cos(40\pi t + \pi )(mm)\). Biết tốc độ truyền sóng trên mặt chất lỏng là $30(cm/s)$. Xét hình vuông $ABCD$ thuộc mặt chất lỏng. Số điểm dao động với biên độ cực đại trên đoạn $BD$ là :
Trả lời bởi giáo viên
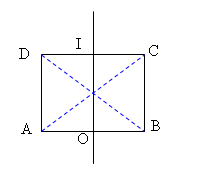
\(BD = \sqrt {A{D^2} + A{B^2}} = 20\sqrt 2 (cm)\)
Với \(\omega = 40\pi (rad/s) \Rightarrow T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{40\pi }} = 0,05(s)\)
Vậy :
\(\lambda = v.T = 30.0,05 = 1,5cm\)
Tìm số điểm dao động với biên độ cực đại trên đoạn $DB$ chứ không phải $DC$.
Nghĩa là điểm $C$ lúc này đóng vai trò là điểm $B$.
Do hai nguồn dao động ngược pha nên số cực đại trên đoạn $BD$ thoã mãn :
\(\left\{ \begin{array}{l}{d_2} - {d_1} = (2k + 1)\dfrac{\lambda }{2}\\AD - BD < {d_2} - {d_1} < AB - 0\end{array} \right.\)
Suy ra :
\(AD - BD < (2k + 1)\dfrac{\lambda }{2} < AB\) Hay : \(\dfrac{{2(AD - BD)}}{\lambda } < 2k + 1 < \dfrac{{2AB}}{\lambda }\). Thay số :
\(\dfrac{{2(20 - 20\sqrt 2 )}}{{1,5}} < 2k + 1 < \dfrac{{2.20}}{{1,5}}\) =>\( - 11,04 < 2k + 1 < 26,67\) Vậy: -6,02<k<12,83. Có $19$ điểm cực đại
Hướng dẫn giải:
+ Áp dụng biểu thức xác định bước sóng: \(\lambda = vT\)
+ Áp dụng điều kiện dao động cực đại của 2 nguồn ngược pha: \({d_2} - {d_1} = (2k + 1)\dfrac{\lambda }{2}\)

