Tại 2 điểm A, B cách nhau 13cm trên mặt nước có 2 nguồn sóng đồng bộ, tạo ra sóng mặt nước có bước sóng là 1,2cm. M là điểm trên mặt nước cách A và B lần lượt là 12cm và 5cm .N đối xứng với M qua AB. Số hyperbol cực đại cắt đoạn MN là :
Trả lời bởi giáo viên
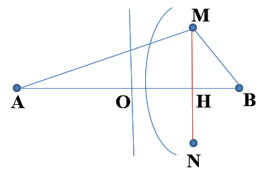
Ta có: \(A{M^2} + M{B^2} = A{B^2}\) \( \Rightarrow \Delta AMB\) vuông tại M.
Từ hình vẽ ta có: \(\cos \angle \left( {{\rm{MAB}}} \right) = {\rm{cos}}\angle \left( {{\rm{MAH}}} \right)\)
\( \Leftrightarrow \dfrac{{AM}}{{AB}} = \dfrac{{AH}}{{AM}} \Rightarrow AH = \dfrac{{A{M^2}}}{{AB}} = \dfrac{{{{12}^2}}}{{13}} = \dfrac{{144}}{{13}}cm\)
Lại có: \(HB = AB - AH = 13 - \dfrac{{144}}{{13}} = \dfrac{{25}}{{13}}cm\)
Số cực đại trên HM thỏa mãn:
\(\begin{array}{l}AH - HB > {d_2} - {d_1} = k\lambda > AM - MB\\ \Leftrightarrow \dfrac{{144}}{{13}} - \dfrac{{25}}{{13}} > 1,2k > 12 - 5 \Leftrightarrow 7,63 > k > 5,83 \Rightarrow k = 6,7\end{array}\)
Vậy có 2 hyperbol cực đại cắt MN.
Hướng dẫn giải:
Áp dụng điều kiện của vân cực đại của 2 nguồn cùng pha: d2 - d1 = kλ

