Hai nguồn sóng kết hợp giống hệt nhau được đặt cách nhau một khoảng cách x trên đường kính của một vòng tròn bán kính \(R\) \((x << R)\) và đối xứng qua tâm của vòng tròn. Biết rằng mỗi nguồn đều phát sóng có bước sóng \(λ\) và \(x = 6λ\). Số điểm dao động cực đại trên vòng tròn là:
Trả lời bởi giáo viên
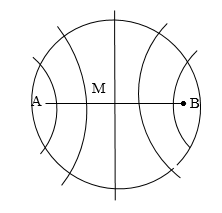
Cách 1: Xét điểm M trên AB (AB = 2x = 12l) AM = d1; BM = d2
d1 – d2 = kλ; d1 + d2 = 6λ;
=> d1 = (3 + 0,5k)λ
0 ≤ d1 = (3 + 0,5k)λ ≤ 6λ
=> - 6 ≤ k ≤ 6
Số điểm dao động cực đại trên AB là 13 điểm kể cả hai nguồn A, B.
Nhưng số đường cực đại cắt đường tròn chỉ có 11 vì vậy, số điểm dao động cực đại trên vòng tròn là 22.
Cách 2: Các vân cực đại gồm các đường hyperbol nhận 2 nguồn làm tiêu điểm nên tại vị trí nguồn không có các hyperbol do đó khi giải bài toán này ta chỉ có
\( - 6\lambda < k\lambda < 6\lambda \)
( không có dấu bằng) nên chỉ có 11 vân cực đại do đó cắt đường tròn 22 điểm cực đại .
Hướng dẫn giải:
Áp dụng điều kiện dao động cực đại của 2 nguồn cùng pha: d2 - d1 = kλ
+ Số điểm dao động trên vòng tròn là 2Ncđ (không tính nguồn)

