Bài tập năng lượng của con lắc lò xo

Cơ năng dao động của con lắc lò xo:

\(W = \dfrac{1}{2}k{A^2} \to A = \sqrt {\dfrac{{2{\rm{W}}}}{k}}  = \sqrt {\dfrac{{2.0,12}}{{150}}}  = 0,04m = 4cm\)

A - sai vì: Động năng của con lắc lò xo:

\(\begin{array}{l}{W_d} = \dfrac{1}{2}m{v^2} = \dfrac{1}{2}m{\omega ^2}{A^2}{\sin ^2}(\omega t + \varphi )\\ = W - {W_t} = \dfrac{1}{2}k{A^2} - \dfrac{1}{2}k{x^2}\end{array}\)

B, C, D - đúng

Động năng và thế năng của vật biến thiên điều hòa với cùng tần số góc 2?, tần số 2f và chu kì T/2.

Cơ năng được bảo toàn

=> C - sai

Khi vật đang chuyển động từ vị trí biên về vị trí cân bằng thì: Thế năng giảm - Động năng tăng - Cơ năng bảo toàn.

Cách 1:

Phương trình vận tốc của vật: v = x’(t) = -50psin(5pt) cm/s    (1)

Tại t = 0,5s thay vào (1) => v = -50p

=> Động năng của vật:

\({{\text{W}}_d} = \frac{1}{2}m{v^2} = \frac{1}{2}.0,2.{(0,5\pi )^2} = 0,25J\)

Cách 2:

Thay t = 0,5s vào phương trình dao động, ta có: x = 0

=> v_max

=> Động năng của vật khi đó chính bằng cơ năng:

\({{\text{W}}_d} = \frac{1}{2}m{v^2} = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}.0,2.{(5\pi .0,1)^2} = 0,25J\)

Tại vị trí có động năng gấp n lần thế năng của vật: W_đ = nW_t

\(\left\{ \begin{array}{l}{W_d} = n{W_t}\\W = {W_t} + {W_d}\end{array} \right. \to \left\{ \begin{array}{l}{W_t} = \dfrac{1}{{n + 1}}W\\{W_d} = \dfrac{n}{{n + 1}}W\end{array} \right. \to \left\{ \begin{array}{l}x =  \pm \dfrac{A}{{\sqrt {n + 1} }}\\v =  \pm A\omega \sqrt {\dfrac{n}{{n + 1}}} \end{array} \right.\)

Từ phương trình dao động điều hòa, ta có: Biên độ dao động A = 10cm

Khi W_đ = 3W_t

\(\left\{ \begin{array}{l}{W_d} = 3{W_t}\\W = {W_t} + {W_d}\end{array} \right. \to {W_t} = \dfrac{1}{{3 + 1}}W \to x =  \pm \dfrac{A}{{\sqrt {3 + 1} }} =  \pm 5cm\)

Từ phương trình dao động điều hòa, ta có:

+ Biên độ A = 10 cm

+ Tần số góc: ω = 4p

Khi W_đ = 3W_t

\(\left\{ \begin{array}{l}{W_t} = 3{W_d}\\W = {W_t} + {W_d}\end{array} \right. \to {W_d} = \dfrac{1}{{3 + 1}}W \to v =  \pm \dfrac{{A\omega }}{{\sqrt {3 + 1} }} =  \pm 20\pi cm/s\)

Khi W_t = 3W_đ

\(\left\{ \begin{array}{l}{W_t} = 3{W_d}\\W = {W_t} + {W_d}\end{array} \right. \to \left\{ \begin{array}{l}{W_t} = \dfrac{3}{{3 + 1}}W\\{W_d} = \dfrac{1}{{3 + 1}}W\end{array} \right. \to \left\{ \begin{array}{l}x =  \pm A\sqrt {\dfrac{3}{{3 + 1}}} \\v =  \pm \dfrac{{A\omega }}{{\sqrt {3 + 1} }}\end{array} \right. \to \dfrac{x}{v} = \dfrac{{\sqrt 3 }}{\omega }\)

Tần số góc:

\(\omega  = 2\pi f = 10\pi (ra{\rm{d}}/s)\)

Tại li độ $x = 2cm$ có:

+ Thế năng:

\({{\rm{W}}_t} = \dfrac{1}{2}k{{\rm{x}}^2} = \dfrac{1}{2}m{\omega ^2}{x^2} = \dfrac{1}{2}0,1.{(10\pi )^2}{(0,02)^2} = 0,02J\)

+ Động năng:

\({{\text{W}}_d} = {\text{W  -  }}{{\text{W}}_t} = 0,08 - 0,02 = 0,06J\)

\(\dfrac{{{{\text{W}}_d}}}{{{{\text{W}}_t}}} = \dfrac{{0,06}}{{0,02}} = 3\)

Khi v = 20%v_max = 0,2 Aω

Áp dụng hệ thức độ lập ta có:

\({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} \to {x^2} = {A^2} - \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2} - \dfrac{{{{(0,2A\omega )}^2}}}{{{\omega ^2}}} = 0,96{A^2}\)

Khi đó, ta có:

+ Động năng của vật: \({{\text{W}}_d} = \dfrac{1}{2}m{v^2} = \dfrac{1}{2}m{(0,2)^2}{\omega ^2}{A^2}\)

+ Thế năng của vật: \({{\rm{W}}_t} = \dfrac{1}{2}k{{\rm{x}}^2} = \dfrac{1}{2}m{\omega ^2}{x^2} = \dfrac{1}{2}m{\omega ^2}0,96.{A^2}\)

\(\dfrac{{{{\text{W}}_d}}}{{{{\text{W}}_t}}} = \dfrac{{\dfrac{1}{2}m{{(0,2)}^2}{\omega ^2}{A^2}}}{{\dfrac{1}{2}m{\omega ^2}0,96.{A^2}}} = \dfrac{1}{{24}}\) 

Ta có:

\({{\text{W}}_t} = {{\text{W}}_d} \to 2{{\text{W}}_t} = {\text{W}} \to x =  \pm \dfrac{A}{{\sqrt 2 }}\)

Ta có, khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là \(\dfrac{T}{4}\)

Vị trí:

\({{\text{W}}_t} = {{\text{W}}_d} \to 2{{\text{W}}_t} = {\text{W}} \to x =  \pm \dfrac{A}{{\sqrt 2 }}\)

=> Khoảng thời gian ngắn nhất kể từ khi vật dao động đến thời điểm mà động năng bằng thế năng là: \(\dfrac{T}{8}\)

Ta có:

\({{\text{W}}_t} = {{\text{W}}_d} \to 2{{\text{W}}_t} = {\text{W}} \to x =  \pm \frac{A}{{\sqrt 2 }}\)

Ta có, khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là \(\dfrac{T}{4}\)

Theo đầu bài, ta có:

\(\begin{array}{l}\dfrac{\pi }{{40}} = \dfrac{T}{4} \to T = \dfrac{\pi }{{10}}\\\omega  = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{\dfrac{\pi }{{10}}}} = 20(ra{\rm{d}}/s)\end{array}\)

Ta có: tần số góc

\(\omega  = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{\dfrac{\pi }{5}}} = 10(ra{\rm{d}}/s)\)

Cơ năng của dao động:

\({\rm{W = }}\dfrac{1}{2}m{\omega ^2}{A^2} \to A = \sqrt {\dfrac{{2{\rm{W}}}}{{m{\omega ^2}}}}  = \sqrt {\dfrac{{2.0,02}}{{1{{(10)}^2}}}}  = 0,02m = 2cm\)

Chu kì dao động của chất điểm:

\(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{4\pi }} = 0,5{\rm{s}}\)

Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\left( { - \dfrac{\pi }{6}} \right) = \dfrac{{A\sqrt 3 }}{2}\\v =  - A\omega \sin \left( { - \dfrac{\pi }{6}} \right) > 0\end{array} \right.\)

Tại vị trí: \({{\text{W}}_t} = {{\text{W}}_d} \to 2{{\text{W}}_t} = {\text{W}} \to x =  \pm \dfrac{A}{{\sqrt 2 }}\)

Ta có: $1s = 2T$

=> Sau $1s$, chất điểm lại quay về vị trí ban đầu

Mặt khác, trong $1$ chu kì chất điểm đi qua li độ mà động năng bằng thế năng $4$ lần

=> Trong $1s (2T)$ chất điểm đi qua li độ có động năng bằng thế năng $2.4 = 8$ lần

Ta có:

+ Cơ năng: \({\rm{W = }}\dfrac{1}{2}m{\omega ^2}{A^2}\)

+ Gia tốc cực đại: \({a_{{\rm{max}}}} = {\omega ^2}A\)

\( \to \dfrac{{\rm{W}}}{{{a_{{\rm{max}}}}}} = \dfrac{{mA}}{2} = \dfrac{{{{2.10}^{ - 3}}}}{{0,8}} = 2,{5.10^{ - 3}} \to A = \dfrac{{2.2,{{5.10}^{ - 3}}}}{m} = \dfrac{{2.2,{{5.10}^{ - 3}}}}{{0,1}} = 0,05m = 5cm\)

thay vào a_max

\( \to \omega  = \sqrt {\dfrac{{{a_{{\rm{max}}}}}}{A}}  = \sqrt {\dfrac{{0,8}}{{0,05}}}  = 4{\rm{r}}a{\rm{d}}/s\)

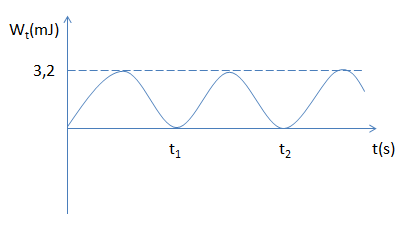
Gọi \(T'\): chu kì tuần hoàn của thế năng

Ta có: \(T' = \dfrac{T}{2}\)

Từ đồ thị Wt - t, ta có:

\(\begin{array}{l}{t_2} - {t_1} = {\rm{ }}0,05s = T' = \dfrac{T}{2} \to T = 0,1s\\ \to \omega  = \dfrac{{2\pi }}{T} = 20\pi \left( {rad/s} \right)\end{array}\)

\({{\rm{W}}_{{t_{{\rm{max}}}}}}{\rm{ = }}\dfrac{1}{2}m{\omega ^2}{A^2} = 3,{2.10^{ - 3}} \to A = \sqrt {\dfrac{{2{{\rm{W}}_{{t_{{\rm{max}}}}}}}}{{m{\omega ^2}}}}  = \sqrt {\dfrac{{2.3,{{2.10}^{ - 3}}}}{{0,1{{(20\pi )}^2}}}}  = {4.10^{ - 3}}m = 0,4cm\)

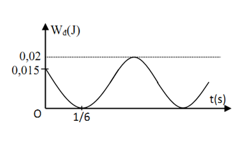
Từ đồ thị, ta có:

+ Tại thời điểm ban đầu (t =0) :

\(\begin{array}{l}{{\rm{W}}_d} = 0,015 \to {{\rm{W}}_t} = 0,02 - 0,015 = {5.10^{ - 3}}J = \dfrac{{\rm{W}}}{4}\\ \to {x_0} =  \pm \dfrac{A}{2}\end{array}\)

+ Vị trí có W_đ = 0 lần thứ nhất: <=> x₁ = ±A

Dựa vào đồ thị ta suy ra: x₀ = A/2 và x₁ = A

=> Khoảng thời gian vật đi từ x₀ đến x₁ là:

\(\Delta t = \dfrac{T}{6} = \dfrac{1}{6}s \to T = 1{\rm{s}} \to \omega  = \dfrac{{2\pi }}{T} = 2\pi (ra{\rm{d}}/s)\)

\({{\rm{W}}_{{{\rm{d}}_{{\rm{max}}}}}} = \dfrac{1}{2}m{\omega ^2}{A^2} = 0,02 \to A = \sqrt {\dfrac{{2{{\rm{W}}_{{d_{{\rm{max}}}}}}}}{{m{\omega ^2}}}}  = \sqrt {\dfrac{{2.0,02}}{{0,4.{{(2\pi )}^2}}}}  = 0,05m = 5cm\)

Tại t = 0:

\(\left\{ \begin{array}{l}{x_0} = Ac{\rm{os}}\varphi {\rm{ = }}\dfrac{A}{2}\\v =  - {\rm{Asin}}\varphi  > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\frac{1}{2}\\\sin \varphi  < 0\end{array} \right. \to \varphi  =  - \dfrac{\pi }{3}\)

=> Phương trình dao động của vật: \(x = 5c{\rm{os}}\left( {2\pi t - \dfrac{\pi }{3}} \right)cm\)

Cơ năng ban đầu của con lắc là: \({\rm{W}} = \dfrac{1}{2}k{A^2}\)

Giữ chặt một phần của lò xo, biên độ mới của con lắc và độ cứng của lò xo:

\(k'A' = kA \Rightarrow k' = \dfrac{{kA}}{{A'}}\)

Cơ năng của con lắc giảm 10%, cơ năng còn lại là:

\(\begin{array}{l}{\rm{W}}' = \dfrac{1}{2}k'A{'^2} = 0,9W = 0,9.\dfrac{1}{2}k{A^2}\\ \Rightarrow \dfrac{{kA}}{{A'}}.A{'^2} = 0,9.k{A^2} \Rightarrow A' = 0,9A = A.90\% \\ \Rightarrow A - A' = A.10\% \end{array}\)