Bài tập năng lượng của con lắc lò xo

Ta có: \({{\rm{W}}_t} = {{\rm{W}}_d} \to 2{{\rm{W}}_t} = {\rm{W}} \to x =  \pm \dfrac{A}{{\sqrt 2 }}\)

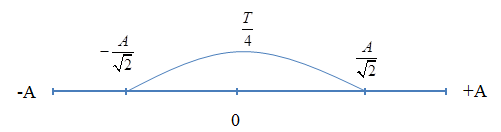
Ta có, khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là \(\dfrac{T}{4}\)

Theo đầu bài, ta có:

\(\begin{array}{l}0,025 = \dfrac{T}{4} \to T = 0,1s\\\omega  = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,1}} = 20\pi (ra{\rm{d}}/s)\end{array}\)

+ Ta có: tần số góc \(\omega  = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,5}} = 4\pi (ra{\rm{d}}/s)\)

+ Cơ năng của dao động: \({\rm{W = }}\dfrac{1}{2}m{\omega ^2}{A^2} \to A = \sqrt {\dfrac{{2{\rm{W}}}}{{m{\omega ^2}}}}  = \sqrt {\dfrac{{2.0,02}}{{0,5{{(4\pi )}^2}}}}  = \sqrt 5 {.10^{ - 2}}m = \sqrt 5 cm\)

+ Chu kì dao động của chất điểm: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{4\pi }} = 0,5{\rm{s}}\)

+ Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\left( { - \dfrac{\pi }{3}} \right) = \dfrac{A}{2}\\v =  - A\omega \sin \left( { - \dfrac{\pi }{3}} \right) > 0\end{array} \right.\)

+ Tại vị trí: \({{\rm{W}}_d} = 3{W_t}\)

\(\begin{array}{l}\left\{ \begin{array}{l}{{\rm{W}}_d} = 3{W_t}\\{{\rm{W}}_t} + {{\rm{W}}_d} = {\rm{W}}\end{array} \right. \to {{\rm{W}}_t} = \dfrac{{\rm{W}}}{4}\\ \to x =  \pm \dfrac{A}{2}\end{array}\)

Ta có: \(\Delta t = 1s = 2.0,5 = 2T\)

=> Sau 1s, chất điểm lại quay về vị trí ban đầu

Mặt khác, trong 1 chu kì chất điểm đi qua li độ mà động năng bằng 3 lần thế năng 4 lần

=> Trong 1s (2T) chất điểm đi qua li độ có động năng bằng 3 lần thế năng 2.4 = 8 lần

Ta có:

+ Cơ năng: \({\rm{W = }}\dfrac{1}{2}m{\omega ^2}{A^2}\)

+ Gia tốc cực đại: \({a_{{\rm{max}}}} = {\omega ^2}A\)

\(\begin{array}{l} \to \dfrac{{\rm{W}}}{{{a_{{\rm{max}}}}}} = \dfrac{{mA}}{2} = \dfrac{{{{2.10}^{ - 3}}}}{{0,5}} = {4.10^{ - 3}}\\ \to A = \dfrac{{{{2.4.10}^{ - 3}}}}{m} = \dfrac{{{{2.4.10}^{ - 3}}}}{{0,16}} = 0,05m = 5cm\end{array}\)

Thay vào a_max \( \to \omega  = \sqrt {\dfrac{{{a_{{\rm{max}}}}}}{A}}  = \sqrt {\dfrac{{0,5}}{{0,05}}}  = \sqrt {10} {\rm{r}}a{\rm{d}}/s\)

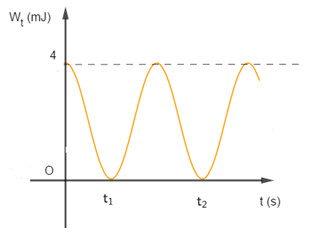
Gọi \(T'\): chu kì tuần hoàn của thế năng

\(T\): chu kì dao động của vật

Ta có: \(T' = \dfrac{T}{2}\)

Từ đồ thị W_t - t, ta có:

\(\begin{array}{l}{t_2} - {t_1} = {\rm{ }}0,02s = T' = \dfrac{T}{2} \to T = 0,04s\\ \to \omega  = \dfrac{{2\pi }}{T} = 50\pi \left( {rad/s} \right)\end{array}\)

\(\begin{array}{l}{{\rm{W}}_{{t_{{\rm{max}}}}}}{\rm{ = }}\dfrac{1}{2}m{\omega ^2}{A^2} = {4.10^{ - 3}}\\ \to A = \sqrt {\dfrac{{2{{\rm{W}}_{{t_{{\rm{max}}}}}}}}{{m{\omega ^2}}}}  = \sqrt {\dfrac{{{{2.4.10}^{ - 3}}}}{{0,16{{(50\pi )}^2}}}}  = \sqrt 2 {.10^{ - 3}}m = \sqrt 2 mm\end{array}\)

Gọi \(T'\): chu kì tuần hoàn của thế năng

\(T\): chu kì dao động của vật

Ta có: \(T' = \dfrac{T}{2}\)

Từ đồ thị W_t - t, ta có:

\(\begin{array}{l}{t_2} - {t_1} = {\rm{ }}0,02s = \dfrac{{T'}}{2} = \dfrac{T}{4} \to T = 0,08s\\ \to \omega  = \dfrac{{2\pi }}{T} = 25\pi \left( {rad/s} \right)\end{array}\)

\(\begin{array}{l}{{\rm{W}}_{{t_{{\rm{max}}}}}}{\rm{ = }}\dfrac{1}{2}m{\omega ^2}{A^2} = {4.10^{ - 3}}\\ \to A = \sqrt {\dfrac{{2{{\rm{W}}_{{t_{{\rm{max}}}}}}}}{{m{\omega ^2}}}}  = \sqrt {\dfrac{{{{2.4.10}^{ - 3}}}}{{0,16{{(25\pi )}^2}}}}  = \sqrt 8 {.10^{ - 3}}m = \sqrt 8 mm\end{array}\)

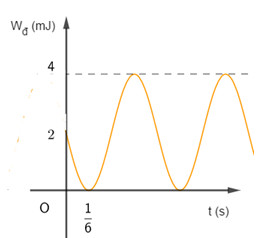
Từ đồ thị, ta có:

+ Tại thời điểm ban đầu (t =0) :

\(\begin{array}{l}{{\rm{W}}_d} = 2mJ \to {{\rm{W}}_t} = 4 - 2 = 2mJ = \dfrac{{\rm{W}}}{2}\\ \to {x_0} =  \pm \dfrac{A}{{\sqrt 2 }}\end{array}\)

+ Vị trí có W_đ = 0 lần thứ nhất \( \leftrightarrow {x_1} =  \pm A\)

Dựa vào đồ thị (động năng đang giảm) ta suy ra: \(\left\{ \begin{array}{l}{x_0} = \dfrac{A}{{\sqrt 2 }}\\{x_1} = A\end{array} \right.\)

=> Khoảng thời gian vật đi từ \({x_0}\) đến \({x_1}\) là: \(\Delta t = \dfrac{T}{8} = \dfrac{1}{6}s \to T = \dfrac{4}{3}{\rm{s}} \to \omega  = \dfrac{{2\pi }}{T} = \dfrac{{3\pi }}{2}(ra{\rm{d}}/s)\)

+ \({{\rm{W}}_{{{\rm{d}}_{{\rm{max}}}}}} = \dfrac{1}{2}m{\omega ^2}{A^2} = 4mJ \to A = \sqrt {\dfrac{{2{{\rm{W}}_{{d_{{\rm{max}}}}}}}}{{m{\omega ^2}}}}  = \sqrt {\dfrac{{{{2.4.10}^{ - 3}}}}{{0,2.{{(\dfrac{{3\pi }}{2} )}^2}}}}  = \dfrac{{\sqrt {10} }}{{75}}m = \dfrac{{4\sqrt {10} }}{3}cm\)

Tại t = 0: \(\left\{ \begin{array}{l}{x_0} = Ac{\rm{os}}\varphi {\rm{ = }}\dfrac{A}{{\sqrt 2 }}\\v =  - {\rm{A}}\omega {\rm{sin}}\varphi  > 0\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi  = \dfrac{1}{{\sqrt 2 }}\\\sin \varphi  < 0\end{array} \right. \to \varphi  =  - \dfrac{\pi }{4}\)

=> Phương trình dao động của vật: \(x = \dfrac{{4\sqrt {10} }}{3}c{\rm{os}}\left( {\dfrac{{3\pi }}{2}t - \dfrac{\pi }{4}} \right)cm\)

+ Khi pha dao động là \(\dfrac{\pi }{2}\) thì vật đạt tốc độ cực đại

=> \({v_{\max }} = 20\sqrt 3 (cm/s)\).

+ \({v_{\max }} = \omega A = \dfrac{{2\pi }}{T}.A \)

\(\to A = \dfrac{{T.{v_{\max }}}}{{2\pi }} = \dfrac{{20\sqrt 3 }}{\pi }(cm)\).

+ Động năng của vật khi li độ \(x = 3π (cm)\) là:

\({W_d} = \dfrac{{k({A^2} - {x^2})}}{2}\\ = \dfrac{{20\left[ {\dfrac{{{{(0,2\sqrt 3 )}^2}}}{{{\pi ^2}}} - {{(0,03\pi )}^2}} \right]}}{2} = 0,03(J)\)

Theo đề bài, ta có:

\(\dfrac{1}{2}k.0,{02^2} + 0,48 = {\rm{W}}\) (1)

\(\dfrac{1}{2}k.0,{06^2} + 0,32 = {\rm{W}}\) (2)

Từ (1) và (2) ta suy ra: \(k = 100N/m\)

Thế vào (1), ta được: \({\rm{W}} = \dfrac{1}{2}.100.0,{02^2} + 0,48 = 0,5J\)

Lại có, \({\rm{W}} = \dfrac{1}{2}k{A^2}\)

Ta suy ra: \(A = \sqrt {\dfrac{{2W}}{k}}  = \sqrt {\dfrac{{2.0,5}}{{100}}}  = 0,1m = 10cm\)

Cơ năng dao động điều hòa: \({\rm{W}} = \frac{1}{2}k{A^2}\)

Thế năng của con lắc khi vật qua li độ x là: \({{\rm{W}}_t} = \dfrac{1}{2}k{x^2}\)

Cơ năng của con lắc lò xo: \({\rm{W}} = \dfrac{1}{2}m{\omega ^2}{A^2}\)

Cơ năng của con lắc là: \({\rm{W}} = \frac{1}{2}m{\omega ^2}{A^2}\)

Cơ năng của con lắc lò xo: \({\rm{W}} = \frac{1}{2}k{{\rm{A}}^2} = \frac{1}{2}m{\omega ^2}{A^2}\)

Cơ năng của con lắc lò xo dao động điều hòa: \(W = \dfrac{1}{2}k{A^2}\)

Ta có, cơ năng của con lắc lò xo dao động điều hòa: \(W = \dfrac{1}{2}k{A^2}\)

=> Cơ năng thỉ lệ thuận với độ cứng k và bình phương biên độ dao động

Ta có, Cơ năng bằng tổng động năng và thế năng mà cơ năng bảo toàn => Động năng tăng bao nhiêu thì thế năng giảm bấy nhiêu và ngược lại.

Ta có, cơ năng của con lắc lò xo

\(W = \dfrac{1}{2}k{A^2}\)

=> Cơ năng của con lắc phụ thuộc vào độ cứng, biên độ dao động của vật

Ta có, cơ năng của con lắc lò xo: \(W = \dfrac{1}{2}k{A^2}\)

=> Khi tăng độ cứng của lò xo lên 4 lần và giảm biên độ dao động 2 lần thì cơ năng của con lắc vẫn không thay đổi

Từ phương trình dao động điều hòa, ta có biên độ $A = 4cm$, tần số góc $\omega = 2$

Cơ năng trong dao động điều hòa của chất điểm:

\(W = \dfrac{1}{2}m{\omega ^2}{A^2} = \dfrac{1}{2}0,{1.2^2}.0,{04^2} = 3,{2.10^{ - 4}}J\)