Câu hỏi:
2 năm trước
Con lắc lò xo dao động theo phương ngang với phương trình \(x = Acos(\omega t + \varphi )\). Cứ sau những khoảng thời gian bằng nhau và bằng \(0,025s\) thì động năng của vật bằng thế năng của lò xo. Con lắc dao động điều hoà với tần số góc
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có: \({{\rm{W}}_t} = {{\rm{W}}_d} \to 2{{\rm{W}}_t} = {\rm{W}} \to x = \pm \dfrac{A}{{\sqrt 2 }}\)
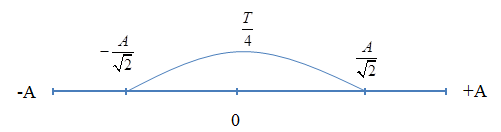
Ta có, khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là \(\dfrac{T}{4}\)
Theo đầu bài, ta có:
\(\begin{array}{l}0,025 = \dfrac{T}{4} \to T = 0,1s\\\omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,1}} = 20\pi (ra{\rm{d}}/s)\end{array}\)
Hướng dẫn giải:
+ Áp dụng biểu thức xác định cơ năng: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_{\rm{d}}}\)
+ Sử dụng trục thời gian suy ra từ vòng tròn
+ Áp dụng biểu thức mối liên hệ giữa tần số góc và chu kì dao động: \(\omega = \dfrac{{2\pi }}{T}\)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
