Câu hỏi:
2 năm trước
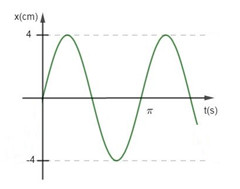
Một con lắc lò xo dao động điều hòa gồm vật nặng có khối lượng \(m = 100g\) , đồ thị thế năng theo thời gian của con lăc như hình vẽ. Biết \({t_2} - {t_1} = 0,05s\), lấy \({\pi ^2} = 10\) . Biên độ và chu kì dao động của con lắc là:
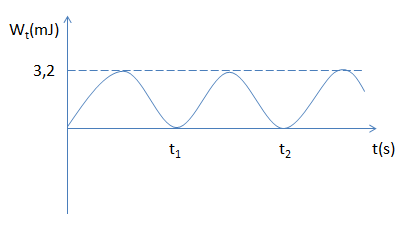
Một con lắc lò xo dao động điều hòa gồm vật nặng có khối lượng \(m = 100g\) , đồ thị thế năng theo thời gian của con lăc như hình vẽ. Biết \({t_2} - {t_1} = 0,05s\), lấy \({\pi ^2} = 10\) . Biên độ và chu kì dao động của con lắc là:
Trả lời bởi giáo viên
Đáp án đúng: c
Gọi \(T'\): chu kì tuần hoàn của thế năng
Ta có: \(T' = \dfrac{T}{2}\)
Từ đồ thị Wt - t, ta có:
\(\begin{array}{l}{t_2} - {t_1} = {\rm{ }}0,05s = T' = \dfrac{T}{2} \to T = 0,1s\\ \to \omega = \dfrac{{2\pi }}{T} = 20\pi \left( {rad/s} \right)\end{array}\)
\({{\rm{W}}_{{t_{{\rm{max}}}}}}{\rm{ = }}\dfrac{1}{2}m{\omega ^2}{A^2} = 3,{2.10^{ - 3}} \to A = \sqrt {\dfrac{{2{{\rm{W}}_{{t_{{\rm{max}}}}}}}}{{m{\omega ^2}}}} = \sqrt {\dfrac{{2.3,{{2.10}^{ - 3}}}}{{0,1{{(20\pi )}^2}}}} = {4.10^{ - 3}}m = 0,4cm\)
Hướng dẫn giải:
+ Đọc đồ thị \({W_t} - {\rm{ }}t\)
+ Thế năng dao động tuần hoàn với chu kì: \(T' = \dfrac{T}{2}\)
+ Áp dụng biểu thức tính thế năng cực đại: \({{\rm{W}}_{{t_{{\rm{max}}}}}}{\rm{ = }}\dfrac{1}{2}m{\omega ^2}{A^2}\)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
