Một vật nặng gắn vào một lò xo nhẹ có độ cứng k = 20 N/m thực hiện dao động điều hoà với biên độ A = 5cm. Động năng của vật khi nó cách vị trí cân bằng 4 cm là
Áp dụng định lí bảo toàn cơ năng cho con lắc, ta có:
\(\begin{align}& \text{W}={{\text{W}}_{t}}+{{\text{W}}_{d}}\Rightarrow \frac{1}{2}k{{A}^{2}}=\frac{1}{2}k{{x}^{2}}+{{\text{W}}_{d}} \\& \Rightarrow {{\text{W}}_{d}}=\frac{1}{2}k{{A}^{2}}-\frac{1}{2}k{{x}^{2}}=0,009\,\,\left( J \right) \\\end{align}\)
Một con lắc lò xo có độ cứng \(k\), khối lượng vật nhỏ \(m\) dao động điều hoà. Tại thời điểm mà li độ và vận tốc của vật tương ứng là \(x\) và \(v\) thì động năng của vật là
Động năng của vật là:\({{\rm{W}}_d} = \frac{1}{2}m{v^2}.\)
Xét một con lắc lò xo gồm vật nhỏ và lò xo nhẹ dao động điều hòa trên mặt phẳng nằm ngang với biên độ A. Chọn gốc thế năng tại vị trí cân bằng. Tại vị trí con lắc có động năng bằng cơ năng, li độ của vật có giá trị là:
Ta có:
\({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t}\)
\( \Leftrightarrow \dfrac{1}{2}k{A^2} = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}k{{\rm{x}}^2}\)
Tại VTCB thế năng bằng 0.
Vị trí con lắc có động năng bằng cơ năng => là vị trí động năng cực đại => VTCB.
Tại VTCB, li độ x = 0.
Động năng dao động của một con lắc lò xo được mô tả theo thế năng dao động của nó bằng đồ thị như hình vẽ. Cho biết khối lượng của vật bằng \(100\,\,g\), vật dao động giữa hai vị trí cách nhau \(8\,\,cm\). Tần số góc của dao động
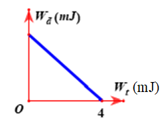
Độ dài quỹ đạo dao động của con lắc là:
\(L = 2A \Rightarrow A = \dfrac{L}{2} = \dfrac{8}{2} = 4\,\,\left( {cm} \right) = 0,04\,\,\left( m \right)\)
Từ đồ thị ta thấy khi động năng bằng 0, thế năng của con lắc:
\(\begin{array}{l}{{\rm{W}}_{t\max }} = \dfrac{1}{2}m{\omega ^2}{A^2} = {4.10^{ - 3}}\,\,\left( J \right)\\ \Rightarrow \dfrac{1}{2}0,1.{\omega ^2}.0,{04^2} = {4.10^{ - 3}} \Rightarrow \omega = 5\sqrt 2 \,\,\left( {rad/s} \right)\end{array}\)

