Một con lắc lò xo dao động điều hòa trên mặt phẳng nằm ngang với chu kì $T=2π (s)$, quả cầu nhỏ có khối lượng M. Khi lò xo có độ dài cực đại và vật M có gia tốc là $-2 (cm/s^2)$ thì một vật có khối lượng $m$ $(M=2m)$ chuyển động dọc theo trục của lò xo đến va chạm đàn hồi xuyên tâm với vật M, có xu hướng làm lò xo nén lại. Biết tốc độ chuyển động của vật m ngay trước lúc va chạm là \(3\sqrt 3 cm/s\). Quãng đường mà vật M đi được từ lúc va chạm đến khi vật $M$ đổi chiều chuyển động là:
Ta có:
\(\left\{ \begin{gathered}
\omega = \frac{{2\pi }}{T} = 1(ra{\text{d}}/s) \hfill \\
{A_0} = \frac{{{a_{{\text{max}}}}}}{{{\omega ^2}}} = \frac{2}{1} = 2cm \hfill \\
V = \frac{{2m{v_0}}}{{m + M}} = \frac{{2.m.3\sqrt 3 }}{{m + 2m}} = 2\sqrt 3 (cm/s) \hfill \\
\end{gathered} \right. \Rightarrow \left\{ \begin{gathered}
{x_0} = - {A_0} \hfill \\
A = \sqrt {x_0^2 + \frac{{{V^2}}}{{{\omega ^2}}}} = \sqrt {{2^2} + \frac{{{{(2\sqrt 3 )}^2}}}{{{1^2}}}} = 4cm \hfill \\
\end{gathered} \right. \to S = A + {A_0} = 6(cm)\)
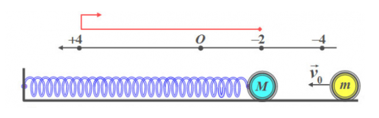
Một con lắc lò xo, vật M đang dao động điều hòa trên mặt phẳng nằm ngang, nhẵn với biên độ A1. Đúng lúc vật M đang ở vị trí biên thì một vật m có khối lượng bằng khối lượng vật M, chuyển động theo phương ngang với vận tốc v0 bằng vận tốc cực đại của vật M, đến va chạm với M. Biết va chạm giữa hai vật là đàn hồi xuyên tâm, sau va chạm vật M tiếp tục dao động điều hòa với biên độ A2. Hệ thức đúng là:
Cách 1:
Ta có:
\(\left\{ \begin{array}{l}{x_0} = \pm {A_1},{v_0} = \omega {A_1}\\V = \frac{{2m{v_0}}}{{m + M}} = \omega {A_1}\end{array} \right. \to {A_2} = \sqrt {x_0^2 + \frac{{{V^2}}}{{{\omega ^2}}}} = {A_1}\sqrt 2 \to \frac{{{A_1}}}{{{A_2}}} = \frac{1}{{\sqrt 2 }}\)
Cách 2: Va chạm tuyệt đối đàn hồi và vì m=M nên m truyền toàn bộ động năng cho M
\(\frac{1}{2}kA_2^2 = \frac{1}{2}kA_1^2 + \frac{1}{2}mv_0^2 \to \frac{1}{2}kA_2^2 = \frac{1}{2}kA_1^2 + \frac{1}{2}kA_1^2 \to A_2^2 = 2A_1^2 \to \frac{{{A_1}}}{{{A_2}}} = \frac{1}{{\sqrt 2 }}\)
Một con lắc lò xo nằm ngang có vật nhỏ khối lượng m1 dao động điều hòa với biên độ A. Khi vật đến vị trí có động năng bằng thế năng thì một vật khác m’ (cùng khối lượng với vật m) rơi thẳng đứng và dính chặt vào vật m thì khi đó 2 vật tiếp tục dao động điều hòa với biên độ:
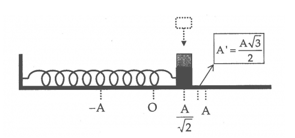
Động năng bằng thế năng
=> \(\left\{ \begin{array}{l}x = \frac{A}{{\sqrt 2 }}\\v = \frac{{{v_{{\rm{max}}}}}}{{\sqrt 2 }} = \frac{{\omega A}}{{\sqrt 2 }}\end{array} \right.\)
Tại đây, m’ va chạm mềm với vật m.
Áp dụng định luật bảo toàn động lượng theo phương ngang:
\(mv = (m + m')v' \to v' = \frac{{mv}}{{m + m'}} = \frac{v}{2} = \frac{{\omega A}}{{2\sqrt 2 }}\)
Tần số góc của hệ hai vật:
\(\omega ' = \sqrt {\frac{k}{{m + m'}}} = \sqrt {\frac{k}{{2m}}} = \frac{\omega }{{\sqrt 2 }}\)
Biên độ của hệ hai vật được tính từ hệ thức độc lập:
\(A' = \sqrt {{x^2} + \frac{{v{'^2}}}{{\omega {'^2}}}} = \sqrt {\frac{{{A^2}}}{2} + \frac{{{A^2}}}{4}} = \frac{{A\sqrt 3 }}{2}\)
Một quả cầu khối lượng $M =2 (kg)$, gắn trên một lò xo nhẹ thẳng đứng có độ cứng $800 (N/m)$, đầu dưới của lò xo gắn cố định. Một vật nhỏ có khối lượng $m=0,4 kg$ rơi tự do từ độ cao $h=1,8m$ xuống va chạm đàn hồi với $M$. Lấy gia tốc trọng trường g =10 m/s2. Sau va chạm, vật $M$ dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo. Biên độ dao động là:
Tốc độ của m ngay trước va chạm:
\({v_0} = \sqrt {2gh} = \sqrt {2.10.1,8} = 6(m/s)\)
Tốc độ của M ngay sau va chạm:
\(V = \frac{{2m{v_0}}}{{m + M}} = \frac{{2.0,4.6}}{{0,4 + 2}} = 2(m/s)\)
Biên độ dao động:
\(A = \frac{V}{\omega } = \frac{V}{{\sqrt {\frac{k}{M}} }} = 0,1m\)
Một con lắc lò xo đặt trên mặt phẳng nằm ngang gồm lò xo nhẹ có một đầu cố định, đầu kia gắn với vật nhỏ m1. Ban đầu giữ vật m1 tại vị trí mà lò xo bị nén 8cm, đặt vật nhỏ m2 (có khối lượng bằng khối lượng vật m1) trên mặt phẳng nằm ngang và sát với vật m1. Buông nhẹ để hai vật bắt đầu chuyển động theo phương của trục lò xo. Bỏ qua mọi ma sát. Ở thời điểm lò xo có chiều dài cực đại lần đầu tiên thì khoảng cách giữa hai vật m1 và m2 là:
Giai đoạn 1: Cả hai vật cùng dao động với biên độ A, tần số góc \(\omega = \sqrt {\frac{k}{{{m_1} + {m_2}}}} \) và tốc độ cực đại v0=ωA.
Giai đoạn 2: Đến VTCB m2 tách ra khỏi m1 thì:
+ m1 dao động điều hòa với tần số góc \(\omega ' = \sqrt {\frac{k}{{{m_1}}}} \) và biên độ \(A' = \frac{{{v_0}}}{{\omega '}} = A\sqrt {\frac{{{m_1}}}{{{m_1} + {m_2}}}} \) (vì tốc độ cực đại không đổi vẫn là v0)
+ m2 chuyển động thẳng đều với vận tốc v0 và khi đến vị trí biên dương (lần 1) thì m2 đi được quãng đường là: \(S = {v_0}\frac{{T'}}{4} = \frac{1}{2}\pi A\sqrt {\frac{{{m_1}}}{{{m_1} + {m_2}}}} \)
Lúc này, khoảng cách hai vật:
\(\Delta x = S - A' = \frac{{\pi A}}{2}\sqrt {\frac{{{m_1}}}{{{m_1} + {m_2}}}} - A\sqrt {\frac{{{m_1}}}{{{m_1} + {m_2}}}} \approx 3,2cm\)
Con lắc lò xo bố trí nằm ngang gồm vật $M =400g$ có thể trượt không ma sát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng vật $m=100 g$ bắn vào M theo phương ngang với tốc độ $1 m/s$, va chạm là hoàn toàn đàn hồi. Sau va chạm vật M dao động điều hòa, chiều dài cực đại và cực tiểu của lò xo lần lượt là $28 cm$ và $20 cm$. Khoảng cách giữa 2 vật sau $1,57s$ từ lúc bắt đầu va chạm là:
Ngay sau va chạm, vận tốc của m và M lần lượt là v và V:
\(\left\{ \begin{array}{l}V = \dfrac{{2m{v_0}}}{{m + M}} = 0,4m/s = 40cm/s\\v = \dfrac{{m - M}}{{m + M}}{v_0} = - 0,6m/s = - 60cm/s\end{array} \right.\)
M dao động điều hòa với tốc độ cực đại V và biên độ:
\(A = \dfrac{{{l_{{\rm{max}}}} - {l_{\min }}}}{2} = 4cm\) nên
\(\omega = \dfrac{V}{A} = 10{\rm{r}}a{\rm{d}}/s \to T = \dfrac{{2\pi }}{\omega } = \dfrac{\pi }{5}s\)
$t=1,57s = 2,5T$
- M ở VTCB
- m đi được quãng đường: $S=vt=60.1,57=94,2cm$
=> Khoảng cách hai vật : $94,2 cm$
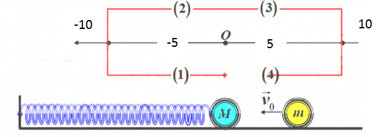
Một con lắc lò xo, lò xo có độ cứng $30 (N/m)$, vật nặng $M=200g$ có thể trượt không ma sát trển mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật $m =100g$ bắn vào $M$ theo phương nằm ngang với tốc độ $3 (m/s)$. Sau va chạm hai vật dính vào nhau và làm cho lò xo nén rồi cùng dao động điều hòa theo phương ngang trùng với trục của lò xo. Gốc thời gian là ngay lúc sau va chạm, thời điểm lần thứ $2013$ và lần thứ $2015$ độ biến dạng của lò xo bằng $5cm$ lần lượt là:
Ta có:
\(\omega = \sqrt {\frac{k}{{m + M}}} = 10(ra{\rm{d}}/s);T = \frac{{2\pi }}{\omega } = \frac{\pi }{5}s\)
\(V = \frac{{m{v_0}}}{{m + M}} = 1(m/s) \to A = \frac{V}{\omega } = 0,1m = 10cm\)
Trong 1 chu kì: lò xo có 4 lần có độ biến dạng bằng 5 cm.
Bốn thời điểm đầu tiên độ biến dạng của lò xo bằng 5cm là:
\(\left\{ \begin{array}{l}{t_1} = \frac{T}{{12}}\\{t_2} = \frac{T}{4} + \frac{T}{6} = \frac{{5T}}{{12}}\\{t_3} = \frac{T}{2} + \frac{T}{{12}} = \frac{{7T}}{{12}}\\{t_4} = \frac{{3T}}{4} + \frac{T}{6} = \frac{{11T}}{{12}}\end{array} \right.\)
Nhận thấy:
\(\left\{ \begin{array}{l}2013 = 503.4 + 1\\2015 = 503.4 + 3\end{array} \right. \to \left\{ \begin{array}{l}{t_{2013}} = 503T + {t_1} = \frac{{6037T}}{{12}} = 316,10{\rm{s}}\\{t_{2015}} = 503T + {t_3} = \frac{{6043T}}{{12}} = 316,41{\rm{s}}\end{array} \right.\)
Một quả cầu khối lượng $M=0,2 kg$, gắn trên một lò xo nhẹ thẳng đứng có độ cứng $20 (N/m)$, đầu dưới của lò xo gắn với đế có khối lượng Mđ. Một vật nhỏ có khối lượng $m=0,1 kg$ rơi tự do từ độ cao $h =0,45 m$ xuống va chạm đàn hồi với M. Lấy gia tốc trọng trường g = 10 m/s2. Sau va chạm vật M dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo. Muốn đế không bị nhấc lên thì Mđ không nhỏ hơn:
Tốc độ của m ngay trước va chạm: \({v_0} = \sqrt {2gh} = \sqrt {2.10.0,45} = 3(m/s)\)
Tốc độ của M ngay sau va chạm: \(V = \frac{{2m{v_0}}}{{m + M}} = \frac{{2.0,1.3}}{{0,1 + 0,2}} = 2(m/s)\)
Biên độ dao động : \(A = \frac{V}{\omega } = \frac{V}{{\sqrt {\frac{k}{M}} }} = 0,2m\)
Muốn đế không bị nhấc lên thì lực kéo cực đại của lò xo (khi vật ở vị trí cao nhất lò xo bị dãn cực đại A-∆l0) không lớn hơn trọng lượng của đế:
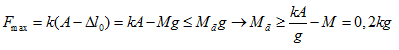
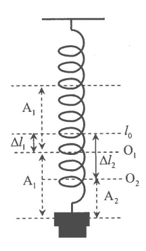
Một con lắc lò xo có độ cứng $k=100 N/m$ và vật nặng khối lượng $M =100 g$, vật dao động điều hòa theo phương thẳng đứng với biên độ $A =4cm$. Khi vật ở biên độ dưới người ta đặt nhẹ nhàng một vật $m=300g$ vào con lắc. Hệ hai vật tiếp tục dao động điều hòa, vận tốc dao động cực đại của hệ là:
- Tại vị trí cân bằng:
Khi vật có khối lượng M thì lò xo dãn:
\(\Delta {l_1} = \frac{{Mg}}{k} = 1cm\)
Khi gắn thêm vật m thì lò xo dãn:
\(\Delta {l_1} = \frac{{(M + m)g}}{k} = 4cm\)
- Khi vật M biên dưới gắn thêm vật m:
Biên độ dao động của hệ vật là: A2=A1+∆l1-∆l2 =1cm
Tần số góc dao động của hệ:
\(\omega ' = \sqrt {\frac{k}{{M + m}}} = \sqrt {\frac{{100}}{{0,1 + 0,3}}} = 5\pi (ra{\rm{d}}/s)\)
=> Vận tốc dao động cực đại của hệ: \({v_{{\rm{max}}}} = \omega '{A_2} = 5\pi .1 = 5\pi (cm/s)\)
Một vật có khối lượng \({m_1} = 125g\) mắc vào lò xo nhẹ có độ cứng $k=200 N/m$, đầu kia của lò xo gắn chặt vào tường, vật và lò xo đặt trên mặt phẳng ngang không ma sát. Đặt vật thứ 2 có khối lượng \({m_2} = 375g\) sát với vật thứ nhất rồi đẩy chậm cả 2 vật cho lò xo nén lại 8cm. Khi thả nhẹ chúng ra, lò xo đẩy 2 vật chuyển động về 1 phía. Lấy \({\pi ^2} = 10\), khi lò xo dãn cực đại lần đầu tiên thì 2 vật cách xa nhau một đoạn là:
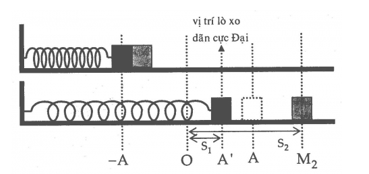
Đẩy chậm lò xo nén lại \(8cm\) rồi thả nhẹ ra => \(A = 8cm\)
Ta có:
+ Tần số góc của hệ hai vật: \(\omega = \sqrt {\dfrac{k}{{{m_1} + {m_2}}}} = \sqrt {\dfrac{{200}}{{0,125 + 0,375}}} = 20\left( {rad/s} \right)\)
+ Tại VTCB vận tốc của hệ có giá trị là \({v_{max}} = A\omega = 160cm/s\) ngay sau đó vận tốc giảm dần nên vật \({m_2}\) tách ra và chuyển động thẳng đều với \(v = {v_{max}}\)
+ Khi \({m_2}\) tách ra, \({m_1}\) dao động với tần số góc \(\omega ' = \sqrt {\dfrac{k}{{{m_1}}}} = \sqrt {\dfrac{{200}}{{0,125}}} = 40\left( {rad/s} \right)\) và chu kì \(T' = \dfrac{{2\pi }}{{\omega '}} = \dfrac{{2\pi }}{{40}} = \dfrac{\pi }{{20}}s\)
+ Thời gian từ lúc hai vật tách ra đến khi lò xo có độ dãn cực đại là thời gian vật \({m_1}\) đi từ VTCB ra biên mới nên mất \(\dfrac{{T'}}{4}\)
Quãng đường \({m_2}\) đi được trong thời gian \(\dfrac{{T'}}{4}\) là: \({S_2} = {v_{{\rm{max}}}}\dfrac{{T'}}{4} = 160.\dfrac{{\dfrac{\pi }{{20}}}}{4} = 2\pi cm\)
Khi \({m_2}\) tách ra thì \({m_1}\) dao động điều hòa với vận tốc cũ nhưng tần số góc thay đổi. Do đó, nó dao động với biên độ: \(A' = \dfrac{{{v_{{\rm{max}}}}}}{{\omega '}} = \dfrac{{{v_{{\rm{max}}}}}}{{\sqrt {\dfrac{k}{{{m_1}}}} }} = 0,04m = 4cm\)
Quãng đường \({m_1}\) đi được trong thời gian \(\dfrac{{T'}}{4}\) là \({S_1} = A' = 4cm\)
Vậy khoảng cách giữa 2 vật khi lò xo dãn cực đại lần đầu tiên là: \(\Delta S = {S_2} - {S_1} = 2\pi - 4cm\)
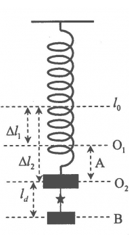
Hai vật $A$ và $B$ có cùng khối lượng $1kg$ và có kích thước nhỏ được nối với nhau bằng một sợi dây mảnh nhẹ dài $10 cm$, hai vật được treo vào lò xo có độ cứng $k =100 N/m$ tại nơi có gia tốc trọng trường \(g = 10{\text{ }}m/{s^2}\) , lấy \({\pi ^2} = 10\). Khi hệ vật và lò xo đang ở vị trí cân bằng đủ cao so với mặt đất, người ta đốt sợi dây nối hai vật và vật $B$ sẽ rơi tự do còn vật $A$ sẽ dao động điều hòa theo phương thẳng đứng. Lần đầu tiên vật $A$ lên đến vị trí cao nhất thì khoảng cách giữa hai vật bằng:
Tại vị trí cân bằng:
Khi chỉ có vật A thì lò xo dãn:
\(\Delta {l_1} = \dfrac{{{m_A}g}}{k} = 10cm\)
Khi treo đồng A và B thì lò xo dãn:
\(\Delta {l_2} = \dfrac{{({m_A} + {m_B})g}}{k} = 20cm\)
Khi hệ vật đang ở VTCB, dây đứt, vật A dao động điều hòa với biên độ A=∆l2-∆l1 = 10 cm.
Chu kỳ con lắc lò xo khi gắn vật A là:
\(T = 2\pi \sqrt {\dfrac{{\Delta {l_1}}}{g}} = 2\pi \sqrt {\dfrac{{0,1}}{{10}}} = \dfrac{\pi }{5}s\)
Thời gian vật A đi từ vị trí đốt dây (biên dưới) đến vị trí cao nhất lần đầu tiên (biên trên ) hết \(t = \dfrac{T}{2} = \dfrac{\pi }{{10}}s\) khi đó, vị trí của vật A là : xA = -A = -10 cm
Sau khi đót dây nối hai vật, vật B rơi tự do từ B cách O1:
O1B = BO2 + O1O2 = ld+A= 20cm
Tọa độ của B:
\({x_B} = {\rm{ }}{O_1}B{\rm{ }} + {\rm{ }}\dfrac{{g{t^2}}}{2} = 0,2 + \dfrac{{10.{{\left( {\dfrac{\pi }{{10}}} \right)}^2}}}{2} = 0,7m = 70cm\)
Vậy khoảng cách giữa hai vật lúc này là: \(\Delta x = {x_B} - {x_A} = 70 - ( - 10) = 80cm\)
Một con lắc lò xo treo thẳng đứng gồm lò xo có độ cứng bằng 100N/m và vật nhỏ khối lượng 250g. Từ vị trí cân bằng, kéo vật xuống dưới một đoạn sao cho lò xo dãn 7,5cm rồi thả nhẹ sau đó vật dao động điều hòa. Lấy \(g = 10m/{s^2}\). Tốc độ của vật khi nó đi qua vị trí lò xo không biến dạng là
Tần số góc: \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{100}}{{0,25}}} = 20rad/s\)
Độ biến dạng của lò xo tại VTCB: \(\Delta l = \frac{{mg}}{k} = \frac{{0,25.10}}{{100}} = 2,5cm\)
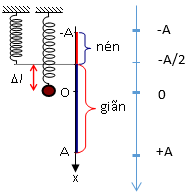
Từ VTCB kéo vật xuống dưới 1 đoạn sao cho lò xo dãn 7,5cm rồi thả nhẹ
\( \Rightarrow \Delta l + A = 7,5cm \Rightarrow A = 7,5 - 2,5 = 5cm\)
Vị trí lò xo không biến dạng có \(\left| x \right| = 2,5cm\)
\( \Rightarrow \) Tốc độ của vât khi nó đi qua vị trí lò xo không biến dạng là:
\(v = \omega \sqrt {{A^2} - {x^2}} = 20\sqrt {{5^2} - 2,{5^2}} = 86,6cm/s\)

