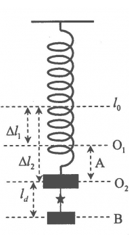
Hai vật $A$ và $B$ có cùng khối lượng $1kg$ và có kích thước nhỏ được nối với nhau bằng một sợi dây mảnh nhẹ dài $10 cm$, hai vật được treo vào lò xo có độ cứng $k =100 N/m$ tại nơi có gia tốc trọng trường \(g = 10{\text{ }}m/{s^2}\) , lấy \({\pi ^2} = 10\). Khi hệ vật và lò xo đang ở vị trí cân bằng đủ cao so với mặt đất, người ta đốt sợi dây nối hai vật và vật $B$ sẽ rơi tự do còn vật $A$ sẽ dao động điều hòa theo phương thẳng đứng. Lần đầu tiên vật $A$ lên đến vị trí cao nhất thì khoảng cách giữa hai vật bằng:

Một con lắc lò xo, lò xo có độ cứng $k =20 (N/m)$, vật nặng $M=100 (g)$ có thể trượt không ma sát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật $m = 100 (g)$ bắn vào M theo phương nằm ngang với tốc độ $3 (m/s)$. Sau va chạm, hai vật dính vào nhau và cùng dao động điều hòa theo phương ngang trùng với trục của lò xo với biên độ là:

Một con lắc lò xo, lò xo có khối lượng không đáng kể, độ cứng $40 (N/m)$, vật nặng $M=400g$ có thể trượt không masát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật $m = 100g$ bắn vào M theo phương nằm ngang với vận tốc $1 (m/s)$. Va chạm là hoàn toàn đàn hồi. Sau khi va chạm vật M dao động điều hòa theo phương ngang với cơ năng là:

Một con lắc lò xo, lò xo có khối lượng không đáng kể, độ cứng $100 (N/m)$, vật nặng $M=300 (g)$ có thể trượt không masát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật $m = 200 (g)$ bắn vào M theo phương nằm ngang với vận tốc $2 (m/s)$. Va chạm là hoàn toàn đàn hồi. Sau khi va chạm, vật M dao động điều hòa theo phương ngang. Gốc tọa độ là điểm cân bằng, gốc thời gian là ngay lúc sau va chạm, chiều dương là chiều lúc bắt đầu dao động. Tính khoảng thời gian ngắn nhất vật có li độ $- 8,8 cm$

Một con lắc lò xo, lò xo có độ cứng .\(k = 80N/m\)., vật nặng \(M = 250g\) có thể trượt không ma sát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật \(m = 150g\) bắn vào M theo phương nằm ngang với tốc độ \(3,2\left( {m/s} \right)\). Sau va chạm, hai vật dính vào nhau và cùng dao động điều hòa theo phương ngang trùng với trục của lò xo với biên độ là:

Một con lắc lò xo, lò xo có khối lượng không đáng kể, độ cứng \(120N/m\), vật nặng \(M = 300g\) có thể trượt không ma sát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật \(m = 100g\) bắn vào M theo phương nằm ngang với vận tốc \(1,5\left( {m/s} \right)\). Va chạm là hoàn toàn đàn hồi. Sau khi va chạm vật M dao động điều hòa theo phương ngang với cơ năng là:

Một con lắc lò xo, lò xo có khối lượng không đáng kể, độ cứng \(k = 80N/m\), vật nặng có khối lượng \(M = 250g\) có thể trượt không ma sát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật có khối lượng \(m = 150g\) bắn vào M theo phương nằm ngang với vận tốc \(2\left( {m/s} \right)\). Va chạm là hoàn toàn đàn hồi. Sau khi va chạm, vật M dao động điều hòa theo phương ngang. Gốc tọa độ là điểm cân bằng, gốc thời gian là ngay lúc sau va chạm, chiều dương là chiều lúc bắt đầu dao động. Tính khoảng thời gian ngắn nhất vật có li độ \( - 8,4cm\)

Một con lắc lò xo, lò xo có độ cứng \(k = 50N/m\), vật nặng có khối lượng \(M = 300g\) có thể trượt không ma sát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật \(m = 200g\) bắn vào M theo phương nằm ngang với tốc độ \(2m/s\). Sau va chạm hai vật dính vào nhau và làm cho lò xo nén rồi cùng dao động điều hòa theo phương ngang trùng với trục của lò xo. Gốc thời gian là ngay lúc sau va chạm, thời điểm lần thứ \(2018\) và lần thứ \(2019\) độ biến dạng của lò xo bằng \(4cm\) lần lượt là: