Một con lắc lò xo, lò xo có độ cứng \(k = 50N/m\), vật nặng có khối lượng \(M = 300g\) có thể trượt không ma sát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật \(m = 200g\) bắn vào M theo phương nằm ngang với tốc độ \(2m/s\). Sau va chạm hai vật dính vào nhau và làm cho lò xo nén rồi cùng dao động điều hòa theo phương ngang trùng với trục của lò xo. Gốc thời gian là ngay lúc sau va chạm, thời điểm lần thứ \(2018\) và lần thứ \(2019\) độ biến dạng của lò xo bằng \(4cm\) lần lượt là:
Trả lời bởi giáo viên
Ta có: \(\omega = \sqrt {\frac{k}{{m + M}}} = \sqrt {\frac{{50}}{{0,3 + 0,2}}} = 10(ra{\rm{d}}/s)\)
+ Chu kì dao động của vật: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{10}} = \frac{\pi }{5}s\)
+ Ta lại có:
\(\begin{array}{l}V = \frac{{m{v_0}}}{{m + M}} = \frac{{0,2.2}}{{0,2 + 0,3}} = 0,8(m/s)\\ \to A = \frac{V}{\omega } = \frac{{0,8}}{{10}} = 0,08m = 8cm\end{array}\)
Trong 1 chu kì: lò xo có 4 lần có độ biến dạng bằng 4 cm.
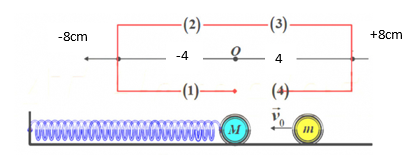
Bốn thời điểm đầu tiên độ biến dạng của lò xo bằng 4cm là: \(\left\{ \begin{array}{l}{t_1} = \frac{T}{{12}}\\{t_2} = \frac{T}{4} + \frac{T}{6} = \frac{{5T}}{{12}}\\{t_3} = \frac{T}{2} + \frac{T}{{12}} = \frac{{7T}}{{12}}\\{t_4} = \frac{{3T}}{4} + \frac{T}{6} = \frac{{11T}}{{12}}\end{array} \right.\)
Nhận thấy: \(\left\{ \begin{array}{l}2018 = 504.4 + 2\\2019 = 504.4 + 3\end{array} \right. \to \left\{ \begin{array}{l}{t_{2018}} = 504T + {t_2} = \frac{{6053T}}{{12}} = 316,93{\rm{s}}\\{t_{2019}} = 504T + {t_3} = \frac{{6055T}}{{12}} = 317,04{\rm{s}}\end{array} \right.\)
Hướng dẫn giải:
+ Vận dụng các công thức trong va chạm mềm của con lắc lò xo nằm ngang.
Va chạm mềm: \(m{v_0} = (m + M)V \Rightarrow V = \frac{1}{{1 + \frac{M}{m}}}{v_0}\)
V: vận tốc của hệ hai vật M+m ở vị trí cân bằng
Nếu sau va chạm cả hai vật dao động điều hòa thì tần số và biên độ dao động của con lắc lò xo:
\(\omega = \sqrt {\frac{k}{{m + M}}} ,A = \frac{V}{\omega }\)
+ Sử dụng biểu thức tính chu kì dao động: \(T = \frac{{2\pi }}{\omega }\)
+ Vận dụng phương pháp giải bài toán “Số lần vật đi qua li độ x”
+ Sử dụng trục thời gian suy ra từ vòng tròn

