Câu hỏi:
2 năm trước
Một con lắc lò xo, lò xo có khối lượng không đáng kể, độ cứng \(k = 80N/m\), vật nặng có khối lượng \(M = 250g\) có thể trượt không ma sát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật có khối lượng \(m = 150g\) bắn vào M theo phương nằm ngang với vận tốc \(2\left( {m/s} \right)\). Va chạm là hoàn toàn đàn hồi. Sau khi va chạm, vật M dao động điều hòa theo phương ngang. Gốc tọa độ là điểm cân bằng, gốc thời gian là ngay lúc sau va chạm, chiều dương là chiều lúc bắt đầu dao động. Tính khoảng thời gian ngắn nhất vật có li độ \( - 8,4cm\)
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có:
V: vận tốc của M ở vị trí cân bằng
Áp dụng định luật bảo toàn động lượng và định lí động năng, ta có:
\(\left\{ \begin{array}{l}m{v_0} = mv + MV\\\frac{1}{2}mv_0^2 = \frac{1}{2}m{v^2} + \frac{1}{2}M{V^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}V = \frac{2}{{1 + \frac{M}{m}}}{v_0}\\v = \frac{{1 - \frac{M}{m}}}{{1 + \frac{M}{m}}}{v_0}\end{array} \right.\)
\(\begin{array}{l}\left\{ \begin{array}{l}V = \frac{{2m{v_0}}}{{m + M}} = \frac{{2.0,15.2}}{{0,15 + 0,25}} = 1,5m/s\\\omega = \sqrt {\frac{k}{M}} = \sqrt {\frac{{80}}{{0,25}}} = 8\sqrt 5 \left( {rad/s} \right)\end{array} \right.\\ \to A = \frac{V}{\omega } = \frac{{1,5}}{{8\sqrt 5 }} \approx 0,084m = 8,4cm\end{array}\)
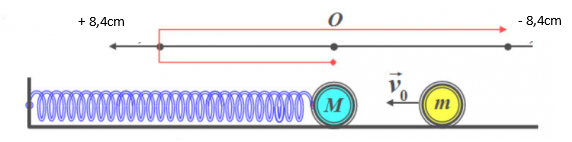
Khoảng thời gian ngắn nhất vật có li độ \( - 8,4cm\) là: \(\Delta t = \frac{{3T}}{4}\)
+ Ta có: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{8\sqrt 5 }} = \frac{{\pi \sqrt 5 }}{{20}}\left( s \right)\)
\( \to \Delta t = \frac{{3T}}{4} = \frac{3}{4}.\frac{{\pi \sqrt 5 }}{{20}} \approx 0,263s\)
Hướng dẫn giải:
Vận dụng các công thức trong va chạm đàn hồi của con lắc lò nằm ngang.
+ Va chạm đàn hồi: \(\left\{ \begin{array}{l}m{v_0} = mv + MV\\\frac{1}{2}mv_0^2 = \frac{1}{2}m{v^2} + \frac{1}{2}M{V^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}V = \frac{2}{{1 + \frac{M}{m}}}{v_0}\\v = \frac{{1 - \frac{M}{m}}}{{1 + \frac{M}{m}}}{v_0}\end{array} \right.\)
V: vận tốc của M ở vị trí cân bằng
+ Sau va chạm M dao động điều hòa: \(\omega = \sqrt {\frac{k}{M}} ,A = \frac{V}{\omega }\)
+ Sử dụng trục thời gian suy ra từ vòng tròn
+ Sử dụng biêu thức tính chu kì: \(T = \frac{{2\pi }}{\omega }\)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
