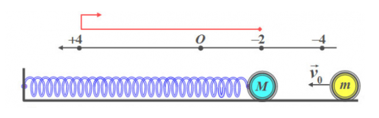
Một con lắc lò xo dao động điều hòa trên mặt phẳng nằm ngang với chu kì $T=2π (s)$, quả cầu nhỏ có khối lượng M. Khi lò xo có độ dài cực đại và vật M có gia tốc là $-2 (cm/s^2)$ thì một vật có khối lượng $m$ $(M=2m)$ chuyển động dọc theo trục của lò xo đến va chạm đàn hồi xuyên tâm với vật M, có xu hướng làm lò xo nén lại. Biết tốc độ chuyển động của vật m ngay trước lúc va chạm là \(3\sqrt 3 cm/s\). Quãng đường mà vật M đi được từ lúc va chạm đến khi vật $M$ đổi chiều chuyển động là:

Một con lắc lò xo, lò xo có độ cứng $k =20 (N/m)$, vật nặng $M=100 (g)$ có thể trượt không ma sát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật $m = 100 (g)$ bắn vào M theo phương nằm ngang với tốc độ $3 (m/s)$. Sau va chạm, hai vật dính vào nhau và cùng dao động điều hòa theo phương ngang trùng với trục của lò xo với biên độ là:

Một con lắc lò xo, lò xo có khối lượng không đáng kể, độ cứng $40 (N/m)$, vật nặng $M=400g$ có thể trượt không masát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật $m = 100g$ bắn vào M theo phương nằm ngang với vận tốc $1 (m/s)$. Va chạm là hoàn toàn đàn hồi. Sau khi va chạm vật M dao động điều hòa theo phương ngang với cơ năng là:

Một con lắc lò xo, lò xo có khối lượng không đáng kể, độ cứng $100 (N/m)$, vật nặng $M=300 (g)$ có thể trượt không masát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật $m = 200 (g)$ bắn vào M theo phương nằm ngang với vận tốc $2 (m/s)$. Va chạm là hoàn toàn đàn hồi. Sau khi va chạm, vật M dao động điều hòa theo phương ngang. Gốc tọa độ là điểm cân bằng, gốc thời gian là ngay lúc sau va chạm, chiều dương là chiều lúc bắt đầu dao động. Tính khoảng thời gian ngắn nhất vật có li độ $- 8,8 cm$

Một con lắc lò xo, lò xo có độ cứng .\(k = 80N/m\)., vật nặng \(M = 250g\) có thể trượt không ma sát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật \(m = 150g\) bắn vào M theo phương nằm ngang với tốc độ \(3,2\left( {m/s} \right)\). Sau va chạm, hai vật dính vào nhau và cùng dao động điều hòa theo phương ngang trùng với trục của lò xo với biên độ là:

Một con lắc lò xo, lò xo có khối lượng không đáng kể, độ cứng \(120N/m\), vật nặng \(M = 300g\) có thể trượt không ma sát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật \(m = 100g\) bắn vào M theo phương nằm ngang với vận tốc \(1,5\left( {m/s} \right)\). Va chạm là hoàn toàn đàn hồi. Sau khi va chạm vật M dao động điều hòa theo phương ngang với cơ năng là:

Một con lắc lò xo, lò xo có khối lượng không đáng kể, độ cứng \(k = 80N/m\), vật nặng có khối lượng \(M = 250g\) có thể trượt không ma sát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật có khối lượng \(m = 150g\) bắn vào M theo phương nằm ngang với vận tốc \(2\left( {m/s} \right)\). Va chạm là hoàn toàn đàn hồi. Sau khi va chạm, vật M dao động điều hòa theo phương ngang. Gốc tọa độ là điểm cân bằng, gốc thời gian là ngay lúc sau va chạm, chiều dương là chiều lúc bắt đầu dao động. Tính khoảng thời gian ngắn nhất vật có li độ \( - 8,4cm\)

Một con lắc lò xo, lò xo có độ cứng \(k = 50N/m\), vật nặng có khối lượng \(M = 300g\) có thể trượt không ma sát trên mặt phẳng nằm ngang. Hệ đang ở trạng thái cân bằng, dùng một vật \(m = 200g\) bắn vào M theo phương nằm ngang với tốc độ \(2m/s\). Sau va chạm hai vật dính vào nhau và làm cho lò xo nén rồi cùng dao động điều hòa theo phương ngang trùng với trục của lò xo. Gốc thời gian là ngay lúc sau va chạm, thời điểm lần thứ \(2018\) và lần thứ \(2019\) độ biến dạng của lò xo bằng \(4cm\) lần lượt là: