Một con lắc lò xo nằm ngang có vật nhỏ khối lượng m1 dao động điều hòa với biên độ A. Khi vật đến vị trí có động năng bằng thế năng thì một vật khác m’ (cùng khối lượng với vật m) rơi thẳng đứng và dính chặt vào vật m thì khi đó 2 vật tiếp tục dao động điều hòa với biên độ:
Trả lời bởi giáo viên
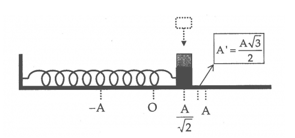
Động năng bằng thế năng
=> \(\left\{ \begin{array}{l}x = \frac{A}{{\sqrt 2 }}\\v = \frac{{{v_{{\rm{max}}}}}}{{\sqrt 2 }} = \frac{{\omega A}}{{\sqrt 2 }}\end{array} \right.\)
Tại đây, m’ va chạm mềm với vật m.
Áp dụng định luật bảo toàn động lượng theo phương ngang:
\(mv = (m + m')v' \to v' = \frac{{mv}}{{m + m'}} = \frac{v}{2} = \frac{{\omega A}}{{2\sqrt 2 }}\)
Tần số góc của hệ hai vật:
\(\omega ' = \sqrt {\frac{k}{{m + m'}}} = \sqrt {\frac{k}{{2m}}} = \frac{\omega }{{\sqrt 2 }}\)
Biên độ của hệ hai vật được tính từ hệ thức độc lập:
\(A' = \sqrt {{x^2} + \frac{{v{'^2}}}{{\omega {'^2}}}} = \sqrt {\frac{{{A^2}}}{2} + \frac{{{A^2}}}{4}} = \frac{{A\sqrt 3 }}{2}\)

