Phát biểu nào sau đây là đúng khi nói về độ lệch pha giữa hai dao động:
Ta có:
+ 2 dao động cùng pha khi:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = k2\pi \)
+ 2 dao động ngược pha khi:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = (2k + 1)\pi \)
+ 2 dao động vuông pha khi:
\(\Delta \varphi = {\varphi _2} - {\varphi _1} = \frac{{2k + 1}}{2}\pi \)
Biên độ dao động khi 2 dao động vuông pha:
\({A^2} = A_1^2 + A_2^2\)
Hai dao động có phương trình lần lượt là: \({x_1} = 5\cos \left( {2\pi t + 0,75\pi } \right)\left( {cm} \right)\) và \({x_2} = 10\cos \left( {2\pi t + 0,5\pi } \right)\left( {cm} \right)\). Độ lệch pha của hai dao động này có độ lớn bằng:
Ta có độ lệch pha giữa hai dao động là:
\(\Delta \varphi = \left| {{\varphi _1} - {\varphi _2}} \right| = \left| {0,75\pi - 0,5\pi } \right| = 0,25\pi \)
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần só có phương trình lần lượt là x1 = A1cos(ωt+φ1) và x2 = A2cos(ωt+φ2). Pha ban đầu của vật được xác định bởi công thức nào sau đây?
Pha ban đầu của 2 dao động tổng hợp:
\(\tan \varphi = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}{\rm{cos}}{\varphi _1} + {A_2}{\rm{cos}}{\varphi _2}}}\)
Xét $2$ dao động điều hòa cùng phương, cùng tần số có phương trình dao động $x_1 = 5cos(3πt + 0,75π)cm$, $x_2= 5sin(3πt – 0,25π)cm$. Pha ban đầu của dao động tổng hợp là:
$x_2 = 5sin(3πt – 0,25π) = 5cos(3πt – 0,75π)cm$
Dao động tổng hợp có pha ban đầu φ được xác định:
\(\tan \varphi = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}{\rm{cos}}{\varphi _1} + {A_2}{\rm{cos}}{\varphi _2}}} = \dfrac{{5.\sin (0,75\pi ) + 5\sin ( - 0,75\pi )}}{{5.c{\rm{os}}(0,75\pi ) + 5c{\rm{os}}( - 0,75\pi )}} \Rightarrow \varphi = \pi \)
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số có phương trình lần lượt là: x1 = A1cos(ωt+φ1) và x2 = A2cos(ωt+φ2). Biên độ dao động A của vật được xác định bởi công thức nào sau đây?
Biên độ dao động tổng hợp A được xác định bởi biểu thức:
\(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos ({\varphi _2} - {\varphi _1})} \)
Cho hai dao động điều hòa cùng phương, cùng tần số, lệch pha nhau một góc π/2 với biên độ A1 và A2. Dao động tổng hợp của hai dao động trên có biên độ là:
Khi đó dao động tổng hợp được xác định bởi biểu thức
\(\begin{array}{l}A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi } ;\Delta \varphi = \frac{\pi }{2}\\ = > A = \sqrt {A_1^2 + A_2^2} \end{array}\)
Phát biểu nào sau đây là sai khi nói về biên độ của dao động tổng hợp của hai dao động điều hoà cùng phương cùng tần số ?
\(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}{\rm{cos}}\Delta \varphi } \)
Biên độ của dao động tổng hợp của hai dao động điều hoà cùng phương cùng tần số không phụ thuộc vào tần số của hai dao động thành phần.
Hai dao động điều hòa cùng phương có phương trình lần lượt là \({x_1} = 4\cos \left( {\pi t - \dfrac{\pi }{6}} \right)\left( {cm} \right)\) và \({x_2} = 4\cos \left( {\pi t - \dfrac{\pi }{2}} \right)\left( {cm} \right)\). Dao động tổng hợp của hai dao động này có biên độ là :
Biên độ dao động tổng hợp:
\({A^2} = A_1^2 + A_2^2 + 2{{\rm{A}}_1}{A_2}\cos \Delta \varphi \)
\( \Leftrightarrow A = \sqrt {{4^2} + {4^2} + 2.4.4.\cos \left| { - \dfrac{\pi }{6} + \dfrac{\pi }{2}} \right|} \)
\( \Leftrightarrow A = \sqrt {48} = 4\sqrt 3 \left( {cm} \right)\)
Một vật thực hiện đồng thời hai dao động điều hoà cùng phương cùng tần số có biên độ lần lượt là A1 = 6 cm và A2 = 12 cm. Biên độ dao động tổng hợp A của vật không thể có giá trị nào sau đây ?
Biên độ dao động tổng hợp thỏa mãn điều kiện:
\(|{A_1} - {A_2}| \le A \le {A_1} + {A_2} \Rightarrow 6 \le A \le 18\)
Biên độ dao động tổng hợp A của vật không thể là 24cm
Hai dao động thành phần có biên độ là 4cm và 12cm. Biên độ dao động tổng hợp có thể nhận giá trị:
Biên độ dao động tổng hợp thỏa mãn điều kiện
\(\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2} \Leftrightarrow 8 \le A \le 16\)
Vậy chỉ có A = 9cm thỏa mãn điều kiện trên
) Một vật khối lượng m = 500g được gắn vào đầu một lò xo nằm ngang. Vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số lần lượt có phương trình x1=6cos(10t+\(\frac{\pi }{2}\))(cm) và x2 = 8cos10t(cm). Năng lượng dao động của vật nặng bằng
Dao động của vật là tổng hợp hai dao động thành phần, có biên độ :
\(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}c{\rm{os}}\left( {{\varphi _1} - {\varphi _2}} \right)} = \sqrt {{6^2} + {8^2}} = 10cm\) = 0,1m
Tần số góc \(\omega \) = 10 rad/s
Vật có m = 500g = 0,5kg.
Năng lượng dao động của vật là:
\({\rm{W}} = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}.0,{5.10^2}.0,{1^2} = 0,25J\)
Một vật thực hiện đồng thời ba dao động điều hoà cùng phương, cùng tần số có phương trình \({x_1} = 4c{\rm{os(10}}\pi {\rm{t + }}\frac{\pi }{4})cm\); \({x_2} = 4c{\rm{os(10}}\pi {\rm{t + }}\frac{{7\pi }}{{12}})cm\) và \({x_3} = 6\sin {\rm{(10}}\pi {\rm{t + }}\frac{\pi }{{12}})cm\). Phương trình dao động tổng hợp của vật là:
Dao động thành phần:
\({x_1} = 4cos(10\pi t + \frac{\pi }{4})(cm)\)
\({x_2} = 4cos(10\pi t + \frac{{7\pi }}{{12}})(cm)\)
\({x_3} = 6\sin (10\pi t + \frac{\pi }{{12}})(cm) = 6c{\rm{os}}(10\pi t - \frac{{5\pi }}{{12}})(cm)\)
Phương trình dao động tổng hợp \(x = {x_1} + {x_2} + {x_3}\)
Ta thấy: \({x_2},{x_3}\) dao động ngược pha nhau
Ta suy ra: \({x_{23}} = {x_2} + {x_3} = 2c{\rm{os}}\left( {10\pi t - \frac{{5\pi }}{{12}}} \right)cm\)
\( \to x = {x_1} + {x_{23}}\)
Độ lệch pha: \(\Delta \varphi = \frac{\pi }{4} + \frac{{5\pi }}{{12}} = \frac{{2\pi }}{3}(ra{\rm{d}})\)
+ Biên độ dao động tổng hợp:
\(\begin{array}{l}A = \sqrt {A_1^2 + A_{23}^2 + 2{A_1}{A_{23}}{\rm{cos}}\Delta \varphi } \\ = \sqrt {{4^2} + {2^2} + 2.4.2{\rm{cos}}\frac{{2\pi }}{3}} = 2\sqrt 3 cm\end{array}\)
+ Pha của dao động tổng hợp:
\(\begin{array}{l}\tan \varphi = \frac{{{A_1}\sin {\varphi _1} + {A_{23}}\sin {\varphi _{23}}}}{{{A_1}{\rm{cos}}{\varphi _1} + {A_{23}}{\rm{cos}}{\varphi _{23}}}}\\ = \frac{{4.\sin \frac{\pi }{4} + 2.\sin \frac{{ - 5\pi }}{{12}}}}{{{\rm{4}}{\rm{.cos}}\frac{\pi }{4} + 2{\rm{cos}}\frac{{ - 5\pi }}{{12}}}} = 2 - \sqrt 3 \\ \to \varphi = {15^0} = \frac{\pi }{{12}}\end{array}\)
=> Phương trình dao động tổng hợp: \(x = 2\sqrt 3 {\rm{cos}}\left( {10\pi t + \frac{\pi }{{12}}} \right)cm\)
Dao động tổng hợp của hai dao động điều hòa cùng phương , cùng tần số có phương trình li độ là x = 3cos(πt - 5π/6) (cm). Biết dao động thứ nhất có phương trình li độ là x1 = 5cos(πt + π/6) (cm). Dao động thứ hai có phương trình li độ là:
Ta có x = x1 + x2 => x2 = x – x1
x = 3cos(πt - 5π/6) (cm).
x1 = 5cos(πt+π/6) (cm) => -x1 = 5cos(πt - 5π/6)
=> x2 = 8cos(πt - 5π/6)(cm)
Một vật nhỏ có chuyển động là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình là \({x_1} = {A_1}\cos \omega t\) và \({x_2} = {A_2}\cos \left( {\omega t + \frac{\pi }{2}} \right)\). Gọi E là cơ năng của vật. Khối lượng của vật bằng
+ Do hai dao động vuông pha nên biên độ dao động tổng hợp là :
\(A = \sqrt {A_1^2 + A_2^2} \)
+ Cơ năng dao động của vật :
\(E = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}m{\omega ^2}(A_1^2 + A_2^2)\)
=> Khối lượng vật
\(m = \frac{{2E}}{{{\omega ^2}(A_1^2 + A_2^2)}}\)
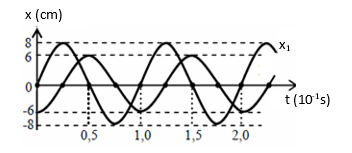
Cho hai dao động điều hoà với li độ x1 và x2 có đồ thị như hình vẽ. Tổng tốc độ của hai dao động ở cùng một thời điểm có giá trị lớn nhất là:
Phương trình chất điểm 1 : là \({x_1} = 8\cos \left( {20\pi t - \frac{\pi }{2}} \right)cm\)
Phương trình chất điểm 2 là :
\({x_2} = 6\cos \left( {20\pi t + \pi } \right)cm\)
Hai chất điểm vuông pha :
\( \Rightarrow A = \sqrt {A_1^2 + A_2^2} = 10\)
Vận tốc lớn nhất :
\({v_{m{\rm{ax}}}} = \omega .A = 20\pi .10 = 200\pi cm/s\)
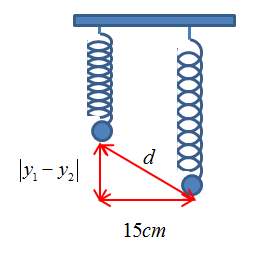
Hai chất điểm dao động trên hai phương song song với nhau và cùng vuông góc với trục \(Ox\) nằm ngang. Vị trí cân bằng của chúng nằm trên \(Ox\) và cách nhau \(15 cm\), phương trình dao động của chúng lần lượt là: \(y_1= 8cos(7πt – π/12)cm\); \(y_2= 6cos(7πt + π/4) cm\). Khoảng cách lớn nhất giữa hai chất điểm gần giá trị nào nhất sau đây:
\({y_1} - {y_2} = 8cos\left( {7\pi t - \dfrac{\pi }{{12}}} \right) - 6cos\left( {7\pi t + \dfrac{\pi }{4}} \right)\)
+ Cách 1: Tổng hợp dao động
\(\begin{array}{l}{y_1} - {y_2} = 8cos\left( {7\pi t - \dfrac{\pi }{{12}}} \right) - 6cos\left( {7\pi t + \dfrac{\pi }{4}} \right)\\ = 8cos\left( {7\pi t - \dfrac{\pi }{{12}}} \right) + 6cos\left( {7\pi t + \dfrac{\pi }{4} + \pi } \right)\end{array}\)
Biên độ dao động tổng hợp: \(A = \sqrt {{8^2} + {6^2} + 2.8.6cos\left( {\pi + \dfrac{\pi }{4} - \left( { - \dfrac{\pi }{{12}}} \right)} \right)} = \sqrt {52} cm\)
\( \Rightarrow {y_1} - {y_2} = \sqrt {52} cos\left( {7\pi t + \varphi } \right)\)
+ Cách 2: Sử dụng máy tính
Bấm \(8\angle - \dfrac{\pi }{{12}} - 6\angle \dfrac{\pi }{4}\) SHIFT 2 3 = \(2\sqrt {13} \angle - 1,066\)
\( \Rightarrow {y_1} - {y_2} = 2\sqrt {13} cos\left( {7\pi t +\varphi} \right)\)
Ta có:
Khoảng cách giữa hai chất điểm: \(d = \sqrt {{{\left( {{y_1} - {y_2}} \right)}^2} + {{15}^2}} \)
Lại có \((y_1-y_2)_{max}=\sqrt{52} =2\sqrt{13}cm\)
=> Khoảng cách lớn nhất giữa hai chất điểm là \(d=\sqrt {52 + {{15}^2}} = 16,6cm\)
Hai con lắc lò xo giống hệt nhau được treo vào hai điểm ở cùng độ cao, cách nhau 3cm. Kích thích cho hai con lắc dao động điều hòa theo phương thẳng đứng với phương trình lần lượt là \({x_1} = 3c{\rm{os}}\left( {\omega t} \right)\) và \({x_2} = 6c{\rm{os}}\left( {\omega t + \frac{\pi }{3}} \right)cm\). Trong quá trình dao động, khoảng cách lớn nhất giữa hai vậ nhỏ của các con lắc bằng:
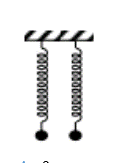
Ta có: Khoảng cách giữa hai vật nhỏ của con lắc bằng:
\(d = \sqrt {{3^2} + {{\left| {{x_1} - {x_2}} \right|}^2}} \)
Ta có:
\({x_1} - {\rm{ }}{x_2} = 3c{\rm{os}}\left( {\omega t} \right) - 6c{\rm{os}}\left( {\omega t + \frac{\pi }{3}} \right) = 3c{\rm{os}}\left( {\omega t} \right) + 6c{\rm{os}}\left( {\omega t + \frac{\pi }{3} + \pi } \right)\)
Biên độ tổng hợp: của x1 - x2 là
\({A^2} = {3^2} + {6^2} + 2.3.6.c{\rm{os(}}\pi {\rm{ + }}\frac{\pi }{3}) \to A \approx 5,2cm\)
\({d_{max}} \leftrightarrow {\left| {{x_1} - {x_2}} \right|_{{\rm{max}}}} = A \to {d_{max}} = \sqrt {{3^2} + {{(5,2)}^2}} = 6cm\)
Một vật có khối lượng không đổi, thực hiện đồng thời hai dao động điều hòa có phương trình dao động lần lượt là \({x_1} = {\rm{ }}10cos\left( {2pt{\rm{ }} + {\rm{ }}\varphi } \right)\) cm và \({x_2} = {A_2}cos(2\pi t - \dfrac{\pi }{2})cm\) thì dao động tổng hợp là \(x = Acos(2\pi t - \dfrac{\pi }{3})cm\). Khi năng lượng dao động của vật cực đại thì biên độ dao động A2 có giá trị là
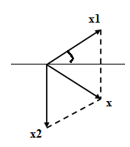
\(\begin{array}{l}\dfrac{{10}}{{\sin 30}} = \dfrac{{{A_2}}}{{\sin (60 + \varphi )}} = \dfrac{A}{{\sin (90 - \varphi )}}\\ \Rightarrow A = \dfrac{{10\sin (90 - \varphi )}}{{\sin 30}}\end{array}\)
Năng lượng dao động cực đại thì \({A_{max}} \Rightarrow \sin \left( {90 - \varphi } \right) = 1 \Rightarrow \varphi = 0\)
Khi đó: \(\left\{ \begin{array}{l}A = \dfrac{{10\sin 90}}{{\sin 30}} = 20cm\\{A_2} = \dfrac{{10.\sin 60}}{{\sin 30}} = 10\sqrt 3 cm\end{array} \right.\)
Hai dao động cùng phương lần lượt có phương trình ${x_1} = {A_1}{\rm{cos(}}\pi {\rm{t + }}\frac{\pi }{6})(cm)$ và ${x_2} = 6{\rm{cos(}}\pi {\rm{t - }}\frac{\pi }{2})(cm)$. Dao động tổng hợp của hai dao động này có phương trình $x = A{\rm{cos(}}\pi {\rm{t + }}\varphi$ (cm). Thay đổi A1 cho đến khi A đạt giá trị cực tiểu thì:
Ta có:
\(\begin{array}{l}\frac{A}{{\sin 60}} = \frac{6}{{\sin (30 + \varphi )}} = \frac{{{A_1}}}{{\sin (90 - \varphi )}}\\ \Rightarrow A = \frac{{6.\sin 60}}{{\sin (30 + \varphi )}}\end{array}\)
Để Amin thì
$\sin (30 + \varphi )max = 1 \to \varphi = {60^0}$
Vậy dao động tổng hợp có pha ban đầu là - 600
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương cùng tần số. Biết dao động thứ nhất có biên độ \(A_1= 6 cm\) và trễ pha \(\dfrac{\pi}{2}\) so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ \(9 cm\). Biên độ dao động tổng hợp bằng:
Dao động tổng hợp: \(x=x_1+x_2\)
Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ \(9 cm\), ta có: \(x_1+6cm=9cm\)
=> \(x_1= 3cm\)
Dựa vào đề bài ta biểu diễn được các véc tơ dao động như hình bên.
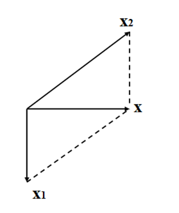
Hai dao động vuông pha nên ta có:
\(\dfrac{{x_1^2}}{{A_1^2}} + \dfrac{{x_{}^2}}{{A_{}^2}} = 1 \Leftrightarrow \dfrac{{{3^2}}}{{{6^2}}} + \dfrac{{{9^2}}}{{{A^2}}} = 1 \Rightarrow A = 6\sqrt 3 cm\)