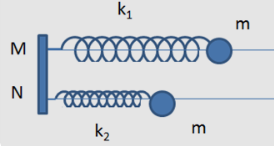
Hai con lắc lò xo giống hệt nhau được treo vào hai điểm ở cùng độ cao, cách nhau 3cm. Kích thích cho hai con lắc dao động điều hòa theo phương thẳng đứng với phương trình lần lượt là \({x_1} = 3c{\rm{os}}\left( {\omega t} \right)\) và \({x_2} = 6c{\rm{os}}\left( {\omega t + \frac{\pi }{3}} \right)cm\). Trong quá trình dao động, khoảng cách lớn nhất giữa hai vậ nhỏ của các con lắc bằng:

Cho hai con lắc lò xo nằm ngang \((k_1, m)\) và \((k_2, m)\) như hình vẽ. Trục dao động M và N cách nhau \(9cm\). Lò xo \(k_1\) có độ cứng \(100 N/m\); chiều dài tự nhiên \(l_1= 35cm\)­. Lò xo \(k_2\)_{­ ­}có độ cứng \(25N/m\), chiều dài tự nhiên \(l_2= 26cm\). Hai vật có khối lượng cùng bằng \(m\). Thời điểm ban đầu (t = 0), giữ lò xo \(k_1\) dãn một đoạn \(3cm\), lò xo \(k_2\) nén một đoạn \(6cm\) rồi đồng thời thả nhẹ để hai vật dao động điều hoà. Bỏ qua mọi ma sát. Khoảng cách nhỏ nhất giữa hai vật trong quá trình dao động xấp xỉ bằng :

Hai dao động điều hoà cùng phương, cùng tần số, cùng pha thì có độ lệch pha bằng

Xét một điểm M bất kì nằm trong miền giao thoa giữa hai sóng được tạo ra bởi hai nguồn kết hợp có cùng phương, cùng tần số, và có biên độ lần lượt là 3 cm và 2 cm. Biên độ dao động của điểm M này không thể nhận giá trị nào sau đây?

Dao động của một vật có khối lượng 100 g là tổng hợp của hai dao động cùng phương có phương trình lần lượt là \({x_1} = 5\cos \left( {10t + \dfrac{\pi }{3}} \right)\left( {cm} \right);{x_2} = 5\cos \left( {10t - \dfrac{\pi }{6}} \right)\left( {cm} \right)\)  (t tính bằng s). Động năng cực đại của vật là

Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số, có đồ thị li độ của các dao động thành phần theo thời gian như hình vẽ. Khi đi qua vị trí cân bằng, vật có tốc độ là

Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số và có cùng biên độ là 4 cm. Nếu biên độ dao động tổng hợp cũng là 4 cm thì độ lớn độ lệch pha của dao động tổng hợp với dao động thành phần là

Cho hai dao động điều hoà cùng phương, cùng tần số, cùng biên độ A và lệch pha nhau $\frac{\pi }{3}.$ Dao động tổng hợp của hai dao động này có biên độ là