Câu hỏi:
2 năm trước
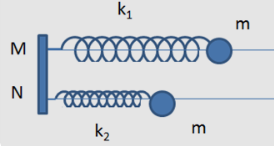
Hai chất điểm dao động trên hai phương song song với nhau và cùng vuông góc với trục \(Ox\) nằm ngang. Vị trí cân bằng của chúng nằm trên \(Ox\) và cách nhau \(15 cm\), phương trình dao động của chúng lần lượt là: \(y_1= 8cos(7πt – π/12)cm\); \(y_2= 6cos(7πt + π/4) cm\). Khoảng cách lớn nhất giữa hai chất điểm gần giá trị nào nhất sau đây:
Trả lời bởi giáo viên
Đáp án đúng: c
\({y_1} - {y_2} = 8cos\left( {7\pi t - \dfrac{\pi }{{12}}} \right) - 6cos\left( {7\pi t + \dfrac{\pi }{4}} \right)\)
+ Cách 1: Tổng hợp dao động
\(\begin{array}{l}{y_1} - {y_2} = 8cos\left( {7\pi t - \dfrac{\pi }{{12}}} \right) - 6cos\left( {7\pi t + \dfrac{\pi }{4}} \right)\\ = 8cos\left( {7\pi t - \dfrac{\pi }{{12}}} \right) + 6cos\left( {7\pi t + \dfrac{\pi }{4} + \pi } \right)\end{array}\)
Biên độ dao động tổng hợp: \(A = \sqrt {{8^2} + {6^2} + 2.8.6cos\left( {\pi + \dfrac{\pi }{4} - \left( { - \dfrac{\pi }{{12}}} \right)} \right)} = \sqrt {52} cm\)
\( \Rightarrow {y_1} - {y_2} = \sqrt {52} cos\left( {7\pi t + \varphi } \right)\)
+ Cách 2: Sử dụng máy tính
Bấm \(8\angle - \dfrac{\pi }{{12}} - 6\angle \dfrac{\pi }{4}\) SHIFT 2 3 = \(2\sqrt {13} \angle - 1,066\)
\( \Rightarrow {y_1} - {y_2} = 2\sqrt {13} cos\left( {7\pi t +\varphi} \right)\)
Ta có:
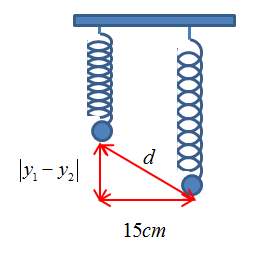
Khoảng cách giữa hai chất điểm: \(d = \sqrt {{{\left( {{y_1} - {y_2}} \right)}^2} + {{15}^2}} \)
Lại có \((y_1-y_2)_{max}=\sqrt{52} =2\sqrt{13}cm\)
=> Khoảng cách lớn nhất giữa hai chất điểm là \(d=\sqrt {52 + {{15}^2}} = 16,6cm\)
Hướng dẫn giải:
Sử dụng lí thuyết về bài toán khoảng cách giữa hai chất điểm dao động điều hoà: $\Delta d = \left| {{d_1} - {d_2}} \right|$
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
