Con lắc lò xo gồm vật m và lò xo $k = 100 N/m$, dao động điều hòa với tần số $3,18 Hz$. Khối lượng vật nặng là:
Ta có, tần số dao động của con lắc lò xo:
\(f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{m}} \to m = \dfrac{k}{{4{\pi ^2}{f^2}}} = \dfrac{{100}}{{4{\pi ^2}{{\left( {3,18} \right)}^2}}} = 0,25kg = 250g\)
Một con lắc lò xo gồm vật nặng có khối lượng $m = 100g$, dao động điều hòa theo phương trình \(x = 5\cos \left( {2\pi t} \right)cm\). Độ cứng của lò xo là:
Từ phương trình dao động của con lắc lò xo, ta có ω = 2p
Mặt khác, ta có:
\(\omega = \sqrt {\dfrac{k}{m}} \to k = m{\omega ^2} = 0,1.{\left( {2\pi } \right)^2} = 4N/m\)
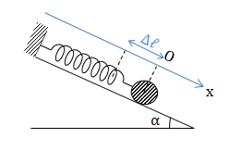
Một con lắc lò xo đặt nằm nghiêng như hình vẽ, vật nặng có khối lượng m, lò xo có độ cứng k. Độ dãn của lò xo tại vị trí cân bằng và chu kì dao động của con lắc lò xo là:
Ta có:
Độ dãn của con lắc lò xo nằm ngang tại vị trí cân bằng: \(\Delta l = \frac{{mg\sin \alpha }}{k}\)
Chu kì do động của con lắc lò xo nằm ngang:
\({\rm{ }}T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{\Delta l}}{{g\sin \alpha }}} \)
Một con lắc lò xo nằm nghiêng dao động điều hòa với chu kì $0,5s$. Biết máng nghiêng góc \(\alpha = {30^0}\), gia tốc rơi tự do $g = {\pi ^2} = 10m/{s^2}$. Độ dãn của lò xo tại vị trí cân bằng là:
Cách 1:
Ta có:
+ Độ dãn của con lắc lò xo nằm nghiêng tại vị trí cân bằng: \(\Delta l = \dfrac{{mg\sin \alpha }}{k}\)
+ Mặt khác, chu kì dao động: \(T = 2\pi \sqrt {\dfrac{m}{k}} \)
=> Độ dãn:
\(\begin{array}{l}\Delta l = \dfrac{{mg\sin \alpha }}{k} = \dfrac{{{T^2}}}{{4{\pi ^2}}}.g\sin \alpha \\ = \dfrac{{{{0,5}^2}}}{{4.10}}.10.\sin 30 = 0,03125m = 3,125cm\end{array}\)
Cách 2:
Ta có, chu kì dao động của con lắc lò xo nằm nghiêng
\({\rm{ }}T = 2\pi \sqrt {\dfrac{{\Delta l}}{{g\sin \alpha }}} \to \Delta l = \dfrac{{{T^2}g\sin \alpha }}{{4{\pi ^2}}} = \dfrac{{0,{5^2}.10.\sin 30}}{{4{\pi ^2}}} = 0,03125m = 3,125cm\)
Con lắc lò xo treo thẳng đứng có độ cứng $k$, khối lượng $m$, \(\Delta l\) là độ dãn của lò xo khi ở vị trí cân bằng, $g$ là gia tốc trọng trường. Chu kì và độ dãn của con lắc lò xo tại vị trí cân bằng là:
Ta có:
Độ dãn của con lắc lò xo treo thẳng đứng tại vị trí cân bằng: \(\Delta l = \dfrac{{mg}}{k}\)
Chu kì dao động của con lắc lò xo treo thẳng đứng:
\(T = 2\pi \sqrt {\dfrac{{\Delta l}}{g}} \)
Một lò xo có chiều dài tự nhiên l0 = 25cm được treo thẳng đứng, treo vật nặng vào dưới lò xo dài l = 27,5cm (lấy g = 10m/s2). Chu kì dao động của con lắc lò xo là:
Ta có độ dãn của lò xo tại vị trí cân bằng:
\(\Delta l = l - {l_0} = 27,5 - 25 = 2,5cm = 0,025m\)
Chu kì dao động của con lắc lò xo treo thẳng đứng:
\(T = 2\pi \sqrt {\frac{{\Delta l}}{g}} = 2\pi \sqrt {\frac{{0,025}}{{10}}} = 0,314s\)
Một lò xo có độ cứng \(k = 25(N/m)\). Một đầu của lò xo gắn vào điểm O cố định. Treo vào lò xo hai vật có khối lượng \(m = 100g\) và \(∆m = 60g\). Tính độ dãn của lò xo khi vật cân bằng và tần số góc dao động của con lắc.
Ta có, độ dãn của lò xo tại vị trí cân bằng:
\(\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,16.10}}{{25}} = 0,064m = 6,4cm\)
Tần số góc dao động của con lắc:
\(\omega = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{{25}}{{0,16}}} = 12,5(ra{\rm{d}}/s)\)
Treo một vật có khối lượng m1 vào con lắc lò xo có độ cứng k thì nó dao động với chu kì T1. Nếu treo quả nặng có khối lượng m2 vào lò xo trên thì nó dao động với chu kì T2. Khi treo cả hai vật vào lò xo thì chúng sẽ dao động với chu kì
Ta có: \(T = 2\pi \sqrt {\frac{m}{k}} \to {T^2} \sim m\)
=> Khi treo cả hai vật vào lò xo thì chu kì dao động là: \(T = \sqrt {T_1^2 + T_2^2} \)
Một con lắc lò xo dao động điều hòa gồm lò xo có độ cứng k và vật có khối lượng m. Khi m = m1 thì chu kì dao động của con lắc là T1, khi m = m2 thì chu kì dao động của con lắc là T2. Khi m = m1 - m2 thì chu kì dao động của con lắc là:
Ta có: \(T = 2\pi \sqrt {\frac{m}{k}} \to {T^2} \sim m\)
=> Khi m = m1 - m2 thì chu kì dao động là: \({T^2} = T_1^2 - T_2^2\)
Con lắc lò xo gồm vật m và lò xo k dao động điều hòa, khi mắc thêm vào vật m một vật khác có khối lượng gấp 3 lần vật m thì chu kì dao động của chúng
Chu kì dao động của hai con lắc:
\(T = 2\pi \sqrt {\dfrac{m}{k}} \)
\(T' = 2\pi \sqrt {\dfrac{{m'}}{k}} = 2\pi \sqrt {\dfrac{{m + 3m}}{k}} = 4\pi \sqrt {\dfrac{m}{k}} \)
\( \to \dfrac{{T'}}{T} = 2\)
Một lò xo có độ cứng k mắc với vật nặng m1 có chu kì dao động T1 = 1,8s. Nếu mắc lò xo đó với vật nặng m2 thì chu kì dao động là T2 = 2,4s. Tìm chu kì dao động khi ghép m1 và m2 với lò xo nói trên:
Ta có, chu kì dao động của vật khi ghép m1 và m2:
\(T = \sqrt {T_1^2 + T_2^2} = \sqrt {1,{8^2} + 2,{4^2}} = 3{\rm{s}}\)
Khi gắn vật có khối lượng m1 = 4kg vào một lò xo có khối lượng không đáng kể, nó dao động với chu kì T1 = 1s. Khi gắn một vật khác có khối lượng m2 vào lò xo trên nó dao động với chu kì T2 = 0,5s. Khối lượng m2 bằng?
Chu kì dao động của vật:
\(T = 2\pi \sqrt {\dfrac{m}{k}} \)
\( \to \dfrac{{{T_1}}}{{{T_2}}} = \sqrt {\dfrac{{{m_1}}}{{{m_2}}}} \to {m_2} = \dfrac{{{m_1}T_2^2}}{{T_1^2}} = \dfrac{{4.0,{5^2}}}{{{1^2}}} = 1kg\)
Lần lượt treo hai vật \(m_1\) và \(m_2\) vào một lò xo có độ cứng \(k = 40N/m\) và kích thích chúng dao động. Trong cùng một khoảng thời gian nhất định, \(m_1\) thực hiện \(20\) dao động và \(m_2\) thực hiện \(10\) dao động. Nếu treo cả hai vật vào lò xo thì chu kì dao động của hệ bằng \(\dfrac{\pi}{2}(s)\). Khối lượng \(m_1\) và \(m_2\) lần lượt bằng bao nhiêu
Ta có: \(T = \dfrac{{\Delta t}}{N} = 2\pi \sqrt {\dfrac{m}{k}} \)
\(\left\{ \begin{array}{l}{T_1} = \dfrac{{\Delta t}}{{20}} = 2\pi \sqrt {\dfrac{{{m_1}}}{k}} \\{T_2} = \dfrac{{\Delta t}}{{10}} = 2\pi \sqrt {\dfrac{{{m_2}}}{k}} \end{array} \right. \to \dfrac{{{T_1}}}{{{T_2}}} = \sqrt {\dfrac{{{m_1}}}{{{m_2}}}} = \dfrac{1}{2} \to {m_2} = 4{m_1}\)
Khi treo cả hai vật:
\(\begin{array}{l}T = 2\pi \sqrt {\dfrac{{{m_1} + {m_2}}}{k}} = 2\pi \sqrt {\dfrac{{5{m_1}}}{k}} \to {m_1} = \dfrac{{{T^2}.k}}{{4{\pi ^2}.5}} = \dfrac{{{{\left( {\dfrac{\pi }{2}} \right)}^2}.40}}{{4{\pi ^2}.5}} = 0,5kg\\ \to {m_2} = 2kg\end{array}\)
Một con lắc lò xo dao động điều hòa gồm lò xo có độ cứng k và vật có khối lượng $m$. Khi $k = k_1$ thì chu kì dao động của con lắc là $T_1$, khi $k = k_2$ thì chu kì dao động của con lắc là $T_2$. Khi mắc nối tiếp $k_1$ với $k_2$ thì chu kì dao động của con lắc là:
Ta có: \(T = 2\pi \sqrt {\dfrac{m}{k}} \to {T^2} \sim \dfrac{1}{k}\)
Nối tiếp \(\dfrac{1}{k} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}}\)
=> cùng treo một vật khối lượng như nhau thì: \({T^2} = T_1^2 + T_2^2\)
Một con lắc lò xo dao động điều hòa gồm lò xo có độ cứng k và vật có khối lượng m. Khi k = k1 thì chu kì dao động của con lắc là T1, khi k = k2 thì chu kì dao động của con lắc là T2. Khi mắc song song k1 với k2 thì chu kì dao động của con lắc là:
Ta có: \(T = 2\pi \sqrt {\dfrac{m}{k}} \to {T^2} \sim \dfrac{1}{k}\)
Song song: k = k1 + k2 Þ cùng treo một vật khối lượng như nhau thì:
\(\dfrac{1}{{{T^2}}} = \dfrac{1}{{T_1^2}} + \dfrac{1}{{T_2^2}}\)
Hai lò xo có chiều dài bằng nhau độ cứng tương ứng là k1, k2. Khi mắc vật m vào một lò xo k1, thì vật m dao động với chu kì T1 = 0,6s. Khi mắc vật m vào lò xo k2, thì vật m dao động với chu kì T2 = 0,8s. Khi mắc vật m vào hệ hai lò xo k1 song song với k2 thì chu kì dao động của m là.
k1, k2 ghép song song, độ cứng của hệ ghép xác định từ công thức: k// = k1 + k2.
Chu kì dao động của con lắc lò xo ghép song song:
\(\dfrac{1}{{{T^2}}} = \dfrac{1}{{T_1^2}} + \dfrac{1}{{T_2^2}} \to T = \sqrt {\dfrac{{T_1^2T_2^2}}{{\left( {T_1^2 + T_2^2} \right)}}} = \sqrt {\dfrac{{0,{6^2}.0,{8^2}}}{{0,{6^2} + 0,{8^2}}}} = 0,48\left( s \right)\)
Hai lò xo có chiều dài bằng nhau độ cứng tương ứng là k1, k2. Khi mắc vật m vào lò xo k1, thì vật m dao động với chu kì T1 = 0,6s. Khi mắc vật m vào lò xo k2, thì vật m dao động với chu kì T2 = 0,8s. Khi mắc vật m vào hệ hai lò xo k1 ghép nối tiếp k2 thì chu kì dao động của m là:
k1, k2 mắc nối tiếp, độ cứng của hệ ghép xác định từ công thức: \(\dfrac{1}{k} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}}\)
Chu kì dao động của con lắ khi ghép nối tiếp 2 lò xo:
\(T = \sqrt {T_1^2 + T_2^2} = \sqrt {0,{6^2} + 0,{8^2}} = 1{\rm{s}}\)
Một con lắc lò xo gồm vật nhỏ khối lượng \(m\) và lò xo có độ cứng \(k\) đang dao động điều hòa với biên độ \(A\).Tốc độ cực đại của vật là:
Tốc độ góc của con lắc: \(\omega = \sqrt {\dfrac{k}{m}} \)
Tốc độ cực đại của vật là \({v_{{\rm{max}}}} = \omega A = A.\sqrt {\dfrac{k}{m}} \)
Một lò xo nhẹ có khối lượng không đáng kể được cắt thành 3 lò xo có chiều dài theo tỉ lệ \(2\):\(2\):\(1\). Vật có khối lượng m được treo vào lò xo thứ nhất thì dãn \(10 cm\). Lấy \(\pi^2 =10\). Nếu treo vật vào lò xo thứ 3 thì chu kì dao động điều hòa của hệ là
+Khi cắt lò xo thành 3 phần, ta có:
\(k\ell = {k_1}{\ell _1} = {k_3}{\ell _3} \\\to \dfrac{{{k_1}2\ell }}{5} = \dfrac{{{k_3}\ell }}{5} \\\to {k_3} = 2{k_1}.\)
+ Khi treo vật vào lò xo thứ nhất, tại vị trí cân bằng ta có: \(mg = {k_1}\Delta {l_1}\)
\( \Rightarrow \dfrac{m}{{{k_1}}} = \dfrac{{\Delta {l_1}}}{g} = \dfrac{{0,1}}{{10}} = 0,01\)
Chu kì dao động khi đó: \({T_1} = 2\pi \sqrt {\dfrac{m}{{{k_1}}}} = 2\pi \sqrt {0,01} = \dfrac{\pi }{5}s = \dfrac{{\sqrt {10} }}{5}s\)
+ Khi treo vật vào lò xo thứ ba, ta có chu kì dao động của vật \({T_3} = 2\pi \sqrt {\dfrac{m}{{{k_3}}}} \)
Ta có: \(\dfrac{{{T_1}}}{{{T_3}}} = \dfrac{{2\pi \sqrt {\dfrac{m}{{{k_1}}}} }}{{2\pi \sqrt {\dfrac{m}{{{k_3}}}} }} = \sqrt {\dfrac{{{k_3}}}{{{k_1}}}} \)
Lại có \(\dfrac{{{k_1}}}{{{k_3}}} = \dfrac{1}{2}\)
Suy ra: \(\dfrac{{{T_1}}}{{{T_3}}} = \sqrt 2 \Rightarrow {T_3} = \dfrac{{{T_1}}}{{\sqrt 2 }} = \dfrac{{\dfrac{{\sqrt {10} }}{5}}}{{\sqrt 2 }} = \dfrac{{\sqrt 5 }}{5}s\)
Một lò xo nhẹ cách điện có độ cứng \(k{\rm{ }} = {\rm{ }}50{\rm{ }}N/m\) một đầu cố định, đầu còn lại gắn vào quả cầu nhỏ tích điện \(q = + 5\mu C\), khối lượng \(m{\rm{ }} = {\rm{ }}200g\). Quả cầu có thể dao động không ma sát dọc theo trục lò xo nằm ngang và cách điện. Tại thời điểm ban đầu t = 0 kéo vật tới vị trí lò xo giãn 4 cm rồi thả nhẹ đến thời điểm t = 0,2 s thì thiết lập điện trường không đổi trong thời gian 0,2 s, biết điện trường nằm ngang dọc theo trục lò xo hướng ra xa điểm cố định và có độ lớn \(E{\rm{ }} = {\rm{ }}{10^5}V/m\) . Lấy \(g{\rm{ }} = {\rm{ }}10m/{s^2}\). trong quá trình dao động thì tốc độ cực đại mà quả cầu đạt được là
Ta có:
+ Chu kì dao động: \(T = 2\pi \sqrt {\dfrac{m}{k}} = 0,4s\)
+ Biên độ dao động ban đầu: \({A_0} = 4cm\)
+ Tại thời điểm \(t = 0\): \(x = 4cm\)
+ Tại thời điểm \(t = 0,2s = \dfrac{T}{2}\): \(x' = 4cm\) và khi đó thiết lập điện trường không đổi trong thời gian \(0,2s\)
Vì \(\overrightarrow E \) hướng ra xa điểm cố định và điện tích \(q > 0\) nên \(\overrightarrow {{F_d}} \uparrow \uparrow \overrightarrow E \)
\( \Rightarrow \) Vị trí cân bằng khi có điện trường lệch ra xa điểm cố định \({x_0} = \dfrac{{qE}}{k} = 0,01m = 1cm\)
\( \Rightarrow \) Biên độ khi có điện trường: \({A_1} = {A_0} + {x_0} = 4 + 1 = 5cm\)
Điện trường không còn sau \(0,2s = \dfrac{T}{2}\) vật sẽ dao động điều hòa quanh vị trí cân bằng ban đầu
\( \Rightarrow \) Biên độ trong giai đoạn này: \({A_2} = {A_1} + {x_0} = 6cm\)
\( \Rightarrow \) Tốc độ cực đại: \({v_{max}} = \omega {A_2} = \dfrac{{2\pi }}{{0,4}}.6 = 30\pi \left( {cm/s} \right)\)

