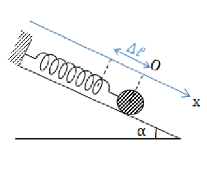
Một con lắc lò xo nằm nghiêng dao động điều hòa với chu kì $0,5s$. Biết máng nghiêng góc \(\alpha = {30^0}\), gia tốc rơi tự do $g = {\pi ^2} = 10m/{s^2}$. Độ dãn của lò xo tại vị trí cân bằng là:
Một con lắc lò xo nằm nghiêng dao động điều hòa với chu kì $0,5s$. Biết máng nghiêng góc \(\alpha = {30^0}\), gia tốc rơi tự do $g = {\pi ^2} = 10m/{s^2}$. Độ dãn của lò xo tại vị trí cân bằng là:
Trả lời bởi giáo viên
Cách 1:
Ta có:
+ Độ dãn của con lắc lò xo nằm nghiêng tại vị trí cân bằng: \(\Delta l = \dfrac{{mg\sin \alpha }}{k}\)
+ Mặt khác, chu kì dao động: \(T = 2\pi \sqrt {\dfrac{m}{k}} \)
=> Độ dãn:
\(\begin{array}{l}\Delta l = \dfrac{{mg\sin \alpha }}{k} = \dfrac{{{T^2}}}{{4{\pi ^2}}}.g\sin \alpha \\ = \dfrac{{{{0,5}^2}}}{{4.10}}.10.\sin 30 = 0,03125m = 3,125cm\end{array}\)
Cách 2:
Ta có, chu kì dao động của con lắc lò xo nằm nghiêng
\({\rm{ }}T = 2\pi \sqrt {\dfrac{{\Delta l}}{{g\sin \alpha }}} \to \Delta l = \dfrac{{{T^2}g\sin \alpha }}{{4{\pi ^2}}} = \dfrac{{0,{5^2}.10.\sin 30}}{{4{\pi ^2}}} = 0,03125m = 3,125cm\)
Hướng dẫn giải:
Cách 1:
+ Vận dụng biểu thức tính độ dãn của con lắc lò xo tại vị trí cân bằng: \(\Delta l = \dfrac{{mg\sin \alpha }}{k}\)
+ Vận dụng biểu thức tính chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {\dfrac{m}{k}} \)
Cách 2:
Áp dụng biểu thức xác chu kì dao động của con lăc lò xo nằm nghiêng:\({\rm{ }}T = 2\pi \sqrt {\dfrac{{\Delta l}}{{g\sin \alpha }}} \)