Sóng âm - Các đặc trưng vật lí và sinh lí của âm

Hai âm có âm sắc khác nhau khi chúng có các họa âm có tần số và biên độ khác nhau

A, C, D đúng

B - sai vì: Cảm giác âm to hay nhỏ phụ thuộc vào cường độ âm và tần số âm

A, B, C đúng

D - sai vì: Trong chất rắn: Sóng âm có thể là sóng dọc hoặc sóng ngang

Họa âm bậc n có: \({f_n} = {\text{ }}n{f_1}\)

Họa âm bậc 2: \({f_2} = {\text{ }}2{f_1}\)

Ta có, chiều dài của dây đàn:

$l = k\dfrac{\lambda }{2} = k\dfrac{v}{{2f}} \to f = k\dfrac{v}{{2l}}$

Âm cơ bản là âm ứng với $k=1$

=> Tần số của âm cơ bản:

${f_1} = \dfrac{v}{{2l}} = \dfrac{{300}}{{2.0,15}} = 1000H{\text{z}}$

=> Bước sóng của âm phát ra trong không khí:

$\lambda  = \dfrac{{{v_{kk}}}}{{{f_1}}} = \dfrac{{340}}{{1000}} = 0,34m$

Khoảng cách giữa người và súng là:

\(L = {\text{ }}500{\text{ }} - {\text{ }}165{\text{ }} = {\text{ }}335m\)

Gọi t₁ là thời gian lúc súng bắt đầu nổ đến tai người:

${t_1} = \dfrac{{{S_1}}}{v} = \dfrac{{335}}{v}$

t₂ là thời gian do âm thanh phản xạ trên bức tường sau khi nghe tiếng nổ:

${t_2} = \dfrac{{{S_2}}}{v} = \dfrac{{500 + 165}}{v}$

Thời gian giữa hai lần tiếng nổ đến tai người là:

$\Delta t = {t_2} - {t_1} = \dfrac{{500 + 165}}{v} - \dfrac{{335}}{v} = \dfrac{{330}}{v} = \dfrac{{330}}{{330}} = 1{\text{s}}$

Các đặc trưng vật lí của sóng âm: tần số, vận tốc, bước sóng, năng lượng âm, cường độ âm và mức cường độ âm.

Các đặc trưng sinh lý của âm gồm: độ cao, độ to và âm sắc

Độ cao phụ thuộc vào tần số của âm.

Tần số lớn  âm bổng

Tần số nhỏ  âm trầm

Ta có:

\(L = \log \dfrac{I}{{{I_0}}}(B) = 10\log \dfrac{I}{{{I_0}}}(dB)\)

Ta có, mức cường độ âm: $L = \log \dfrac{I}{{{I_0}}} = \log \dfrac{{{{10}^{ - 5}}}}{{{{10}^{ - 12}}}} = 7B = 70dB$

Gọi công suất mỗi nguồi là P

Cường độ âm tại B do A gây ra:

${I_{AB}} = \dfrac{{4P}}{{4\pi {d^2}}} = {10^{ - 6}}W/{m^2}$

Cường độ âm tại B do C gây ra:

${I_{CB}} = \dfrac{{6P}}{{4\pi {{(\dfrac{{2d}}{3})}^2}}} = \dfrac{{4P}}{{4\pi {d^2}}}\dfrac{{27}}{8} = 3,{375.10^{ - 6}}W/{m^2}$

$ \to {L_B} = \log \dfrac{{{I_{CB}}}}{{{{10}^{ - 12}}}} = 6,528B = 65,28dB$

Giả sử M cách nguồn âm ban đầu O một khoảng x

+ TH nguồn âm đặt tại O

${L_N} = 10dB \Leftrightarrow 10\lg \frac{{{I_N}}}{{{I_0}}} = 10 \Leftrightarrow {I_N} = 10{I_0}$

Ta có

${L_M} - {L_N} = 20\lg \frac{{{r_N}}}{{{r_M}}} \Leftrightarrow \frac{{{r_N}}}{{{r_M}}} = 10 \Leftrightarrow \frac{{x + a}}{x} = 10 \Rightarrow a = 9x$

+ Khi nguồn âm đặt tại M

Do $I = \frac{P}{{4\pi {r^2}}}$ ,

công suất của nguồn âm không đổi nên

\(\frac{{{I_{2N}}}}{{{I_{1N}}}} = \frac{{{r_{1N}}^2}}{{{r_{2N}}^2}} = \frac{{{{\left( {x + a} \right)}^2}}}{{{a^2}}} = \frac{{{{10}^2}}}{{{9^2}}} \Rightarrow {I_{2N}} = \frac{{{{10}^2}}}{{{9^2}}}{I_{1N}} = \frac{{{{10}^2}}}{{{9^2}}}.10{I_0}\)

Mức độ cường tại N là:

${L_{2N}} = 10\lg \frac{{{I_{2N}}}}{{{I_0}}} = 10\lg \frac{{{I_{2N}}}}{{{I_0}}} = 10\lg \frac{{\frac{{{{10}^2}}}{{{9^2}}}.10{I_0}}}{{{I_0}}} = 10,92dB$ ≈ 11dB

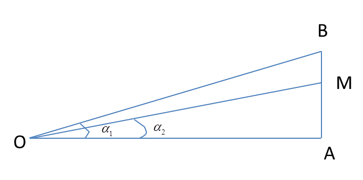
OA = d m

AB = 6 m

AM = 4,5 m

\(\begin{gathered}\tan  = \tan ({\alpha _1} - {\alpha _2}) = \dfrac{{\tan {\alpha _1} - \tan {\alpha _2}}}{{1 +\tan {\alpha _1}\tan {\alpha _2}}} \hfill \\= \dfrac{{\dfrac{6}{d} - \dfrac{{4,5}}{d}}}{{1 + \dfrac{6}{d}.\dfrac{{4,5}}{d}}} = \dfrac{{1,5}}{{d + \dfrac{{27}}{d}}} \hfill \\\end{gathered} \)

Theo BĐT Cosi, ta có:

\(\begin{gathered}d + \dfrac{{27}}{d} \geqslant 2\sqrt {27}  = 2.3\sqrt 3  \hfill \\\to d = 3\sqrt 3 m \hfill \\ \end{gathered} \)

Do đó:

$OM = \sqrt {{{(3\sqrt 3 )}^2} + 4,{5^2}}  = \dfrac{{3\sqrt {21} }}{2}m$

Ta có:

\({L_A} - {L_M} = 10\log \dfrac{{{I_A}}}{{{I_M}}} \leftrightarrow 40 - 50 =  - 10 = 10\log \dfrac{{{I_A}}}{{{I_M}}} \to \dfrac{{{I_A}}}{{{I_M}}} = 0,1\)

Mặt khác:

$\begin{gathered}\left\{ \begin{gathered}{I_A} = \dfrac{{2P}}{{4\pi R_A^2}} \hfill \\{I_M} = \dfrac{{(x + 2)P}}{{4\pi R_M^2}} \hfill \\\end{gathered}  \right. \to \frac{{{I_A}}}{{{I_M}}} = \dfrac{2}{{x + 2}}\frac{{R_M^2}}{{R_A^2}} = \dfrac{2}{{x + 2}}\dfrac{{{{(\dfrac{{3\sqrt {21} }}{2})}^2}}}{{{{(3\sqrt 3 )}^2}}} = 0,1\hfill \\\to x = 33 \hfill \\\end{gathered} $

Quãng đường âm truyền chính là chiều dài của ống gang: \(S = {\rm{l}} = 951,25\,\,m\)

Thời gian âm truyền trong gang là: \({t_1} = \dfrac{S}{{{v_1}}} = \dfrac{{\rm{l}}}{{{v_1}}}\)

Thời gian âm truyền trong không khí là: \({t_2} = \dfrac{S}{{{v_2}}} = \dfrac{{\rm{l}}}{{{v_2}}}\)

Nhận xét: \({v_1} > {v_2} \Rightarrow {t_1} < {t_2}\)

Theo đề bài ta có:

\(\begin{array}{l}{t_2} = {t_1} + 2,5 \Rightarrow {t_2} - {t_1} = 2,5\\ \Rightarrow \dfrac{l}{{{v_2}}} - \dfrac{l}{{{v_1}}} = 2,5 \Rightarrow \dfrac{{951,25}}{{340}} - \dfrac{{951,25}}{{{v_1}}} = 2,5\\ \Rightarrow {v_1} = 3194,32 \approx 3194\,\,\left( {m/s} \right)\end{array}\)

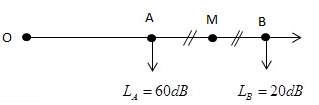
M là trung điểm của AB nên:

\(OM = \dfrac{{OA + OB}}{2} \Rightarrow {r_M} = \dfrac{{{r_A} + {r_B}}}{2}\)

Ta có: \(\left\{ \begin{array}{l}{L_A} = 10.\log \dfrac{P}{{4\pi r_A^2.{I_0}}} = 60dB\\{L_B} = 10.\log \dfrac{P}{{4\pi r_B^2.{I_0}}} = 20dB\\{L_M} = 10.\log \dfrac{P}{{4\pi r_M^2.{I_0}}}\end{array} \right.\)

\(\begin{array}{l} \Rightarrow {L_A} - {L_B} = 10.\log {\left( {\dfrac{{{r_B}}}{{{r_A}}}} \right)^2} = 20 \Rightarrow \log \dfrac{{{r_B}}}{{{r_A}}} = 2 \Rightarrow \dfrac{{{r_B}}}{{{r_A}}} = 100\\ \Rightarrow {r_M} = \dfrac{{{r_A} + 100{r_A}}}{2} = 50,5.{r_A}\end{array}\)

\(\begin{array}{l} \Rightarrow {L_A} - {L_M} = 10.\log {\left( {\dfrac{{{r_M}}}{{{r_A}}}} \right)^2}\\ \Leftrightarrow 60 - {L_M} = 10.\log 50,{5^2} \Rightarrow {L_M} \approx 26dB\end{array}\)

Mức cường độ âm:   \(L = 10\log \frac{I}{{{I_0}}}\)

Ta có:  

\(\left\{ \begin{array}{l}
{L_1} = 10\log \frac{{{I_1}}}{{{I_0}}} = 70dB \Rightarrow {I_1} = {I_0}{.10^7}\,\left( {W/{m^2}} \right)\\
{L_2} = 10\log \frac{{{I_2}}}{{{I_0}}} = 60dB \Rightarrow {I_2} = {I_0}{.10^7}\,\left( {W/{m^2}} \right)
\end{array} \right.\)

Khi một điểm nhận được nhiều âm thanh từ các nguồn khác nhau đến thì cường độ âm nhận được:

\(I = \sum {{I_i}} = {I_1} + {I_2} = {I_0}.\left( {{{10}^7} + {{10}^6}} \right)\)

Mức cường độ âm toàn phần:

\(L = 10\log \frac{I}{{{I_0}}} = 10\log \frac{{{I_0}.\left( {{{10}^7} + {{10}^6}} \right)}}{{{I_0}}} = 70,{41_{}}dB\)

Mức cường độ âm trong nhà máy không vượt quá 85dB. Ta có:

\(\begin{gathered}
L \leqslant 85dB \Leftrightarrow 10.\log \frac{I}{{{I_0}}} \leqslant 85dB \Leftrightarrow \log \frac{I}{{{I_0}}} \leqslant 8,5 \hfill \\
\Rightarrow \frac{I}{{{I_0}}} \leqslant {10^{8,5}} \Rightarrow I \leqslant {10^{8,5}}.{I_0} = {10^{8,5}}{.10^{ - 12}} = {3,16.10^{ - 4}} \hfill \\
\Rightarrow {I_{\max }} = {3,16.10^{ - 4}}\,\,\left( {{\text{W}}/{m^2}} \right) \hfill \\
\end{gathered} \)

→ Cường độ âm cực đại mà nhà máy đó quy định là \({{3,16.10}^{-4}}~W/{{m}^{2}}\)

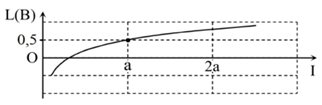
Từ đồ thị ta thấy khi \(I=a\) thì \(L=0,5\,\left( B \right)\)

Áp dụng công thức tính mức cường độ âm ta có:

\(L\,\left( B \right)=\log \frac{I}{{{I}_{0}}}\Rightarrow \frac{I}{{{I}_{0}}}={{10}^{L}}\Rightarrow {{I}_{0}}=\frac{I}{{{10}^{L}}}=\frac{a}{{{10}^{0,5}}}=0,316a\)

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}L = 10.\log \dfrac{I}{{{I_0}}}\,\,\left( {dB} \right)\\L' = 10.\log \dfrac{{I'}}{{{I_0}}}\,\,\left( {dB} \right) = 10.\log \dfrac{{1000.I}}{{{I_0}}} = 10.\log 1000 + 10.\log \dfrac{I}{{{I_0}}}\,\end{array} \right.\\ \Rightarrow L' = L + 30\,\left( {dB} \right)\end{array}\)