Độ to của âm có mối liên hệ với đặc trưng vật lí nào của âm?
Ta có, mối liên hệ giữa đặc trưng sinh lí và đặc trưng vật lí của âm:

Thuật ngữ âm “trầm” , “bổng” chỉ đặc tính nào của âm dưới đây?
Ta có độ cao phụ thuộc vào tần số của âm.
Tần số lớn \( \to \) âm bổng
Tần số nhỏ \( \to \) âm trầm
Một sóng âm có cường độ âm chuẩn là \({I_0}\). Mức cường độ âm, cường độ âm tại vị trí 1 và 2 lần lượt là \({L_1};{I_1}\) và \({L_2};{I_2}\). Hiệu mức cường độ âm của vị trí 2 so với 1 được tính bằng công thức:
Ta có, mức cường độ âm tại 2 vị trí:
(1) \({L_1} = \log \dfrac{{{I_1}}}{{{I_0}}}\)
(2) \({L_2} = \log \dfrac{{{I_2}}}{{{I_0}}}\)
=> Hiệu mức cường độ âm của 2 vị trí:
\({L_2} - {L_1} = \log \dfrac{{{I_2}}}{{{I_0}}} - log\dfrac{{{I_1}}}{{{I_0}}} = \log \dfrac{{\dfrac{{{I_2}}}{{{I_0}}}}}{{\dfrac{{{I_1}}}{{{I_0}}}}} = \log \dfrac{{{I_2}}}{{{I_1}}}\)
Sóng cơ học lan truyền trong không khí với cường độ đủ lớn, tai ta có thể cảm thụ được sóng cơ học nào?
Tai ta có thể nghe được sóng có tần số từ 20 Hz đến 20000 Hz \( \Rightarrow \) loại A, D.
Sóng có chu kì \({\rm{2,0 \mu s }} \Rightarrow f = \dfrac{{\rm{1}}}{{\rm{T}}} = \dfrac{1}{{{{2.10}^{ - 6}}}} = {5.10^5}{\rm{ (Hz)}} \Rightarrow \)loại B
Sóng có chu kì \({\rm{2,0 ms }} \Rightarrow f = \dfrac{{\rm{1}}}{{\rm{T}}} = \dfrac{1}{{{{2.10}^{ - 3}}}} = {5.10^2}{\rm{ (Hz)}} \Rightarrow \)Chọn C
Cường độ âm tại một điểm trong môi trường truyền âm là \({10^{ - 7}}W/{m^2}\). Biết cường độ âm chuẩn là \({10^{ - 12}}W/{m^2}\). Mức cường độ âm tại điểm đó bằng:
Cường độ âm tại điểm đó:
\(L = \log \frac{I}{{{I_0}}} = \log \frac{{{{10}^{ - 7}}}}{{{{10}^{ - 12}}}} = 5B = 50dB\)
Có một số nguồn âm giống nhau với công suất phát âm không đổi trong môi trường đẳng hướng không hấp thụ âm. Nếu tại điểm A đặt \(6\) nguồn âm thì tại điểm B cách A một đoạn \(d\) có mức cường độ âm là \(60dB\). Nếu tại điểm C cách B một đoạn \(\dfrac{d}{3}\) đặt \(9\) nguồn âm thì tại điểm B có mức cường độ âm bằng:
Gọi công suất mỗi nguồi là P
+ Cường độ âm tại B do A gây ra: \({I_{AB}} = \dfrac{{6P}}{{4\pi {d^2}}}\) (1)
Cường độ âm tại B do C gây ra: \({I_{CB}} = \dfrac{{9P}}{{4\pi \dfrac{{{d^2}}}{9}}}\) (2)
Mặt khác, ta có:
\(\begin{array}{l}{L_{AB}} = 10\log \dfrac{{{I_{AB}}}}{{{I_0}}} = 60dB\\ \to \log \dfrac{{{I_{AB}}}}{{{I_0}}} = 6 \to {I_{AB}} = {10^6}{I_0}\end{array}\)
Lại có: \(\dfrac{{{I_{AB}}}}{{{I_{CB}}}} = \dfrac{{\dfrac{{6P}}{{4\pi {d^2}}}}}{{\dfrac{{9P}}{{4\pi \dfrac{{{d^2}}}{9}}}}} = \dfrac{2}{{27}} \to {I_{CB}} = \dfrac{{27}}{2}{I_{AB}} = \dfrac{{27}}{2}{.10^6}{I_0}\)
Ta suy ra, mức cường độ âm do C gây ra tại B:
\({L_{CB}} = 10\log \dfrac{{{I_{CB}}}}{{{I_0}}} = 10\log \dfrac{{\dfrac{{27}}{2}{{.10}^6}{I_0}}}{{{I_0}}} \approx 71,3dB\)
Hai điểm M, N nằm cùng một phía của nguồn âm, trên cùng một phương truyền âm cách nhau một khoảng bằng a, có mức cường độ âm lần lượt là \({L_M} = 50dB\) và \({L_N} = 30dB\). Biết nguồn âm đẳng hướng. Nếu nguồn âm đó đặt tại điểm M thì mức cường độ âm tại N là:
Giả sử M cách nguồn âm ban đầu O một khoảng x
+ Khi nguồn âm đặt tại O, ta có:
\({L_N} = 30dB \Leftrightarrow 10\log \frac{{{I_N}}}{{{I_0}}} = 30 \Leftrightarrow {I_N} = {10^3}{I_0}\)
Ta có:
\(\begin{array}{l}{L_M} - {L_N} = 50 - 30 = 10\log {\left( {\frac{{{r_N}}}{{{r_M}}}} \right)^2}\\ \Leftrightarrow 20 = 20\log \frac{{{r_N}}}{{{r_M}}}\\ \Leftrightarrow \log \frac{{{r_N}}}{{{r_M}}} = 1\\ \Leftrightarrow \frac{{{r_N}}}{{{r_M}}} = 10\\ \Leftrightarrow \frac{{x + a}}{x} = 10\\ \Rightarrow a = 9x\end{array}\)
+ Khi nguồn âm đặt tại M
Do \(I = \frac{P}{{4\pi {r^2}}}\) , công suất của nguồn âm không đổi nên:
\(\begin{array}{l}\frac{{{I_{2N}}}}{{{I_{1N}}}} = \frac{{{r_{1N}}^2}}{{{r_{2N}}^2}} = \frac{{{{\left( {x + a} \right)}^2}}}{{{a^2}}} = \frac{{{{\left( {x + 9x} \right)}^2}}}{{{{\left( {9x} \right)}^2}}} = \frac{{{{10}^2}}}{{{9^2}}}\\ \Rightarrow {I_{2N}} = \frac{{{{10}^2}}}{{{9^2}}}{I_{1N}} = \frac{{{{10}^2}}}{{{9^2}}}{.10^3}{I_0}\end{array}\)
Mức độ cường tại N là: \({L_{2N}} = 10\log \frac{{{I_{2N}}}}{{{I_0}}} = 10\log \frac{{{I_{2N}}}}{{{I_0}}} = 10\log \frac{{\frac{{{{10}^2}}}{{{9^2}}}{{.10}^3}{I_0}}}{{{I_0}}} = 30,92dB \approx 31dB\)
Có nhiều nguồn âm điểm giống hệt nhau và cùng công suất. Ban đầu tại điểm O đặt \(2\) nguồn âm. Điểm A cách O một khoảng d có thể thay đổi được. Trên tia vuông góc với OA tại A, lấy điểm B cách A khoảng \(9cm\). Điểm M nằm trong đoạn AB sao cho \(AM = 4,5cm\) và góc MOB có giá trị lớn nhất, lúc này mức cường độ âm tại A là \({L_A} = 60dB\). Cần phải đặt thêm tại O bao nhiêu nguồn nữa để mức cường độ âm tại M là \(80dB\)
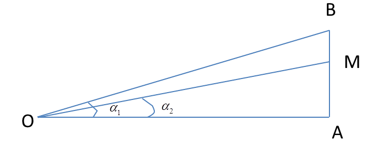
\(\begin{array}{l}\begin{array}{*{20}{l}}{OA = dm}\\{AB = {\rm{ 9}}m}\end{array}\\AM{\rm{ }} = 4,5m\end{array}\)
\(\begin{array}{l}\tan \angle MOB = \tan ({\alpha _1} - {\alpha _2}) = \frac{{\tan {\alpha _1} - \tan {\alpha _2}}}{{1 + \tan {\alpha _1}\tan {\alpha _2}}}\\ = \frac{{\frac{9}{d} - \frac{{4,5}}{d}}}{{1 + \frac{9}{d}.\frac{{4,5}}{d}}} = \frac{{4,5}}{{d + \frac{{81}}{{2d}}}}\end{array}\)
+ Theo BĐT Cosi, ta có:
\(d + \frac{{81}}{{2d}} \ge 2\sqrt {\frac{{81}}{2}} = 9\sqrt 2 \)
Dấu “=” xảy ra khi: \(d = \frac{{81}}{2}d \to d = 4,5\sqrt 2 m\)
Do đó: \(OM = \sqrt {{{(4,5\sqrt 2 )}^2} + 4,{5^2}} = 4,5\sqrt 3 m\)
+ Ta có:
\(\begin{array}{l}{L_A} - {L_M} = 10\log \frac{{{I_A}}}{{{I_M}}}\\ \leftrightarrow 60 - 80 = - 20 = 10\log \frac{{{I_A}}}{{{I_M}}}\\ \to \frac{{{I_A}}}{{{I_M}}} = 0,01\end{array}\)
Mặt khác:
\(\begin{array}{l}\left\{ \begin{array}{l}{I_A} = \frac{{2P}}{{4\pi R_A^2}}\\{I_M} = \frac{{(x + 2)P}}{{4\pi R_M^2}}\end{array} \right.\\ \to \frac{{{I_A}}}{{{I_M}}} = \frac{2}{{x + 2}}\frac{{R_M^2}}{{R_A^2}} = \frac{2}{{x + 2}}\frac{{{{\left( {4,5\sqrt 3 } \right)}^2}}}{{{{\left( {4,5\sqrt 2 } \right)}^2}}} = 0,01\\ \to x = 298\end{array}\)
Cho một nguồn điểm phát sóng âm tại điểm O trong môi trường đẳng hướng và không hấp thụ âm. Hai điểm A, B tạo thành tam giác vuông tại O, cách O lần lượt là 12 m và 15 m. Cho một máy thu di chuyển trên đoạn thẳng AB. Độ chênh giữa mức cường độ âm lớn nhất và nhỏ nhất trong quá trình di chuyển giữa hai điểm A, B là
Ta có hình vẽ:
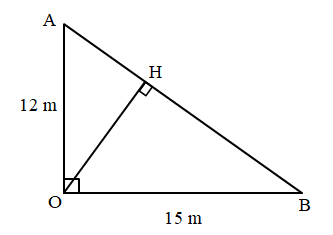
Ta có cường độ âm: \(I = \dfrac{P}{{4\pi {r^2}}} \Rightarrow I \sim \dfrac{1}{{{r^2}}}\)
→ Mức cường độ âm lớn nhất khi máy thu ở tại H, mức cường độ âm nhỏ nhất khi máy thu tại B
Do ∆ABC vuông tại O, ta có:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} = {12^2} + {15^2} \Rightarrow AB = \sqrt {369} = 3\sqrt {41} \,\,\left( m \right)\\OH = \dfrac{{OA.OB}}{{AB}} = \dfrac{{12.15}}{{3\sqrt {41} }} = \dfrac{{60}}{{\sqrt {41} }}\,\,\left( m \right)\end{array}\)
Hiệu mức cường độ âm tại M và B là:
\({L_H} - {L_B} = 10\lg \dfrac{{{I_H}}}{{{I_B}}} = 10\lg \dfrac{{O{B^2}}}{{O{H^2}}} = 10\lg \dfrac{{{{15}^2}}}{{{{\left( {\dfrac{{60}}{{\sqrt {41} }}} \right)}^2}}} \approx 4,1\,\,\left( {dB} \right)\)
Cho cường độ âm do một máy bay phản lực sinh ra trong giai đoạn chuẩn bị cất cánh tại vị trí của quan sát viên là \(3,{16.10^{ - 2}}{\rm{W}}/{m^2}\). Biết cường độ âm chuẩn là \({10^{ - 12}}{\rm{W}}/{m^2}\). Mức cường độ âm tại vị trí của quan sát viên là:
Mức cường độ âm tại vị trí của quan sát viên là:
\(L = 10\log \dfrac{{3,{{16.10}^{ - 2}}}}{{{{10}^{ - 12}}}} = 105{\rm{d}}B\)
Hai điểm A, B nằm trên cùng một đường thẳng đi qua một nguồn âm và ở hai phía so với nguồn âm. Biết mức cường độ âm tại A và tại trung điểm của AB lần lượt là 50dB và 47dB. Mức cường độ âm tại B là
A,B nằm hai phía so với nguồn âm.
Có \({L_A} > {L_M} \Rightarrow OM > OA \Rightarrow \) B và M nằm cùng phía so với nguồn âm.

M là trung điểm của AB nên:
\(OM = AM - OA = \frac{{OB + OA}}{2} - OA = \frac{{OB - OA}}{2}\)
\( \Rightarrow OB = 2.OM + OA\)
Lại có: \(\left\{ \begin{array}{l}{L_A} = 10.\log \frac{P}{{4\pi .O{A^2}.{I_0}}} = 50dB\\{L_B} = 10.\log \frac{P}{{4\pi .O{B^2}.{I_0}}}\\{L_M} = 10.\log \frac{P}{{4\pi .O{M^2}.{I_0}}} = 47dB\end{array} \right.\)
\( \Rightarrow {L_A} - {L_M} = 10\log \frac{{O{M^2}}}{{O{A^2}}} = 3 \Rightarrow OM = 1,4.OA\)
\( \Rightarrow OB = 2.OM + OA = 3,8.OA\)
Lại có: \({L_A} - {L_B} = 10.\log \frac{{O{B^2}}}{{O{A^2}}}\)
\( \Leftrightarrow 50 - {L_B} = 20.\log \frac{{3,8.OA}}{{OA}}\)
\( \Leftrightarrow {L_B} = 50 - 20.\log 3,8 = 38,4dB\)
Sóng âm là
Sóng âm là những sóng cơ học truyền trong các môi trường khí, lỏng, rắn.
Sóng âm trong môi trường lỏng, khí là sóng dọc; trong môi trường rắn là sóng dọc hoặc sóng ngang.
Âm không truyền được trong chân không.
Nhận xét nào sau đây là sai khi nói về sóng âm
Sóng âm trong môi trường lỏng, khí là sóng dọc; trong môi trường rắn là sóng dọc hoặc sóng ngang.
Âm nghe được là sóng cơ học có tần số nằm trong khoảng:
Âm nghe được (âm thanh) là sóng cơ học có tần số nằm trong khoảng $16 Hz- 20000 Hz$
Vận tốc truyền âm trong môi trường nào sau đây là lớn nhất?
Vận tốc truyền âm phụ thuộc vào tính đàn hồi, mật độ của môi trường và nhiệt độ của môi trường.
$v_R > v_L >v_K$
Một lá thép mỏng, một đầu cố định, đầu còn lại được kích thích để dao động với chu kì không đổi và bằng $0,08 s$. Âm do lá thép phát ra là:
Ta có:
$f = \dfrac{1}{T} = \dfrac{1}{{0,08}} = 12,5H{\text{z < 16Hz}}$
=> Hạ âm
Sóng cơ học lan truyền trong không khí với cường độ đủ lớn, tai ta có thể cảm thụ được sóng cơ học nào sau đây:
Ta có:Âm nghe được có tần số từ 16 Hz - 20000 Hz
Tần số âm $f = \dfrac{1}{T}$
A: f = 500kHz
B: f = 500Hz
C: f = 30kHz
D: f =10Hz
Tốc độ truyền âm
Vận tốc truyền âm phụ thuộc vào tính đàn hồi, mật độ của môi trường và nhiệt độ của môi trường.
vR > vL > vK
Khi âm thanh truyền từ không khí vào nước, bước sóng và tần số của âm thanh có thay đổi không?
Khi âm truyền từ môi trường này sang môi trường khác thì vận tốc truyền âm thay đổi, bước sóng của sóng âm thay đổi còn tần số của âm thì không thay đổi.
Khi đi vào một ngõ hẹp, ta nghe tiếng bước chân vọng lại đó là do hiện tượng
Ta nghe tiếng bước chân vọng lại đó là do hiện tượng phản xạ sóng

