Sóng âm - Các đặc trưng vật lí và sinh lí của âm

Giả sử nguồn âm đặt tại O, cách tâm hình vuông đoạn d

Hình vuông có chu vi 400m nên mỗi cạnh có chiều dài 100m

Vì có hai vị trí có cường độ âm lớn nhất và bằng nhau nên OA = OB và mức cường độ âm lớn nhất đo được tại A và B,  mức cường độ âm nhỏ nhất đo được tại C

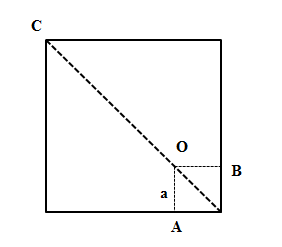
Ta có: \({{I}_{A}}={{I}_{B}}=\frac{P}{4\pi {{a}^{2}}}={{I}_{0}}{{.10}^{\frac{{{L}_{1}}}{10}}}\) (1)

\({{I}_{C}}=\frac{P}{4\pi .{{(100\sqrt{2}-a\sqrt{2})}^{2}}}={{I}_{0}}{{.10}^{\frac{{{L}_{2}}}{10}}}\) (2)

Vì L₁ = L₂ + 10 (dB) \(\Rightarrow \frac{{{L}_{1}}}{10}=\frac{{{L}_{2}}}{10}+1\Rightarrow {{10}^{\frac{{{L}_{1}}}{10}}}={{10}^{\frac{{{L}_{2}}}{10}}}.10\) (3)

Từ (1), (2) và (3) ta được : \(\frac{{{(100\sqrt{2}-a\sqrt{2})}^{2}}}{{{a}^{2}}}=10\Rightarrow a=31m\)

Vậy khoảng cách từ O đến tâm hình vuông là \(50\sqrt{2}-31\sqrt{2}=26,9m\)

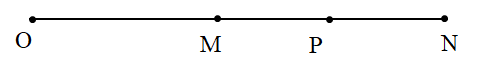
Khi đặt nguồn âm tại O, hiệu mức cường độ âm tại M và N là:

\(\begin{array}{l}{L_M} - {L_N} = 10\log \dfrac{{O{N^2}}}{{O{M^2}}} \Rightarrow 70 - 30 = 10\log \dfrac{{O{N^2}}}{{O{M^2}}}\\ \Rightarrow \dfrac{{ON}}{{OM}} = 100 \Rightarrow ON = 100OM\\ \Rightarrow MN = ON - OM = 100OM - OM = 99OM\\ \Rightarrow MP = \dfrac{{MN}}{2} = \dfrac{{99OM}}{2} = 49,5OM\end{array}\)

Hiệu mức cường độ âm tại M và P là:

\(\begin{array}{l}{L_M} - {L_P} = 10\log \dfrac{{M{P^2}}}{{O{M^2}}}\\ \Rightarrow 70 - {L_P} = 10\log \dfrac{{{{\left( {49,5OM} \right)}^2}}}{{O{M^2}}} \Rightarrow {L_P} \approx 36,1\,\,\left( {dB} \right)\end{array}\)

Từ phương trình sóng ta có: $\Delta \varphi =\dfrac{2\pi x}{\lambda }=kx\Rightarrow \lambda =\dfrac{2\pi }{k}$

Lại có: $\omega =f\Rightarrow T=\dfrac{2\pi }{\omega }=\dfrac{2\pi }{f}$

Vận tốc sóng âm là: $v=\dfrac{\lambda }{T}=\dfrac{\dfrac{2\pi }{k}}{\dfrac{2\pi }{f}}=\dfrac{f}{k}.$

Ta có hiệu hai mức cường độ âm:

$\begin{align}& {{L}_{A}}-{{L}_{B}}=10\log \frac{{{I}_{A}}}{{{I}_{B}}}=10\log {{\left( \frac{OB}{OA} \right)}^{2}} \\& \Rightarrow 55-35=10\log {{\left( \frac{OB}{OA} \right)}^{2}}=20 \\& \Rightarrow \log {{\left( \frac{OB}{OA} \right)}^{2}}=2\Rightarrow {{\left( \frac{OB}{OA} \right)}^{2}}={{10}^{2}} \\& \Rightarrow OB=10OA=50\,\,\left( m \right) \\\end{align}$

Độ to của âm gắn liền với mức cường độ âm

Khi con ruồi và con muỗi bay, ta nghe được tiếng vo ve từ muỗi bay mà không nghe được từ ruồi là do tần số đập cánh của muỗi nằm trong khoảng từ 16 Hz đến 20 000 Hz

Mức cường độ âm tại khu dân cư trức và sau khii chuyển xưởng gỗ là:

\(\begin{array}{l}{L_1} = 10\lg \frac{{{I_1}}}{{{I_0}}} = 110\,\,\left( {dB} \right)\\{L_2} = 10\lg \frac{{{I_2}}}{{{I_0}}} \le 90\,\,\left( {dB} \right)\\ \Rightarrow {L_1} - {L_2} = 10\lg \frac{{{I_1}}}{{{I_2}}} \ge 20\,\,\left( {dB} \right) \Rightarrow \lg \frac{{{I_1}}}{{{I_2}}} \ge 2\end{array}\)

Lại có: \(I = \frac{P}{{4\pi {r^2}}} \Rightarrow I \sim \frac{1}{{{r^2}}}\)

\( \Rightarrow \lg \frac{{{I_1}}}{{{I_2}}} = \lg \frac{{{r_2}^2}}{{{r_1}^2}} \ge 2 \Rightarrow \frac{{{r_2}^2}}{{{r_1}^2}} \ge 100 \Rightarrow {r_2} = 10{r_1} = 1000\,\,\left( m \right)\)

Mỗi cây đàn dây thường có dây được căng trên một hộp đàn có hình dạng và kích thước khác nhau. Hộp đàn có tác dụng như một hộp cộng hưởng sẽ tăng cường âm cơ bản và một số hoạ âm giúp cho âm tổng hợp phát ra vừa to vừa có một âm sắc riêng của đàn.

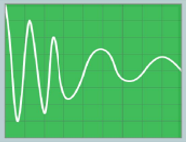
Nhận xét: cường độ âm thanh: 

\(\left\{ {\begin{array}{*{20}{l}}
{I \sim \dfrac{1}{{{r^2}}}}\\
{I \sim {A^2}}
\end{array}} \right. \Rightarrow {A^2} \sim \dfrac{1}{{{r^2}}}\)

\( \Rightarrow \) Càng ra xa nguồn âm, biên độ âm càng giảm.

Từ đồ thị ta thấy biên độ âm giảm dần \( \Rightarrow \) xe cứu thương đang chạy ra xa.

Nhận xét thêm:

Từ đồ thị ta thấy chu kì của âm tăng dần \( \Rightarrow \) tần số f giảm

Tần số của máy thu được khi nguồn âm chuyển động là:

\(f = \dfrac{v}{{v + {v_n}}}{f_0} \Rightarrow \) nguồn âm chuyển động ra xa máy thu

Hình chiếu của vật này lên trục \(Ox\) có biên độ là:

\(A = \frac{d}{2} = 25\,\,\left( {cm} \right) = 0,25\,\,\left( m \right)\)

Ở thời điểm đầu, mức cường độ âm đo được là nhỏ nhất:

\({L_{\min }} \Rightarrow {I_{\min }} \Rightarrow {r_{\max }} = 1,25\,\,\left( m \right) \to \) vật ở vị trí biên xa nhất so với điểm \(H\)

Áp dụng công thức độc lập với thời gian, ta có:

\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow {x^2} + \frac{{{{\left( {1,25\sqrt 3 } \right)}^2}}}{{{{10}^2}}} = 0,{25^2} \Rightarrow x =  \pm 0,125\,\,\left( m \right)\)

Trong một chu kì, có \(4\) lần vật đạt tốc độ \(1,25\sqrt 3 \,\,m/s\)

Ta có vòng tròn lượng giác:

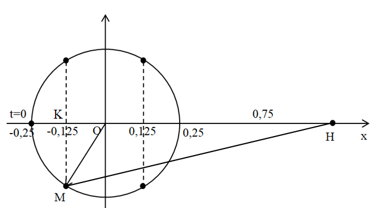
Từ vòng tròn lượng giác ta thấy vật có tốc độ \(1,25\sqrt 3 \,\,m/s\) lần thứ \(2021\) khi vật đi qua li độ \( - 0,125\,\,m\)

Khoảng cách từ điểm \(M\) tới điểm \(H\) là:

\(\begin{array}{l}r = MH = \sqrt {M{K^2} + K{H^2}}  = \sqrt {\left( {O{M^2} - O{K^2}} \right) + {{\left( {OH + OK} \right)}^2}} \\ \Rightarrow r = \sqrt {\left( {0,{{25}^2} - 0,{{125}^2}} \right) + {{\left( {1 + 0,125} \right)}^2}}  \approx 1,1456\,\,\left( m \right)\end{array}\)

Ta có hiệu mức cường độ âm:

\(\begin{array}{l}L - {L_{\min }} = \lg \frac{I}{{{I_{\min }}}} = \lg \frac{{{r_{\max }}^2}}{{{r^2}}}\\ \Rightarrow L - 5 = \lg \frac{{1,{{25}^2}}}{{1,{{1456}^2}}} \Rightarrow L \approx 5,076\,\,\left( B \right) = 50,76\,\,\left( {dB} \right)\end{array}\)

Cường độ âm có giá trị gần nhất với giá trị \(50,8\,\,dB\)

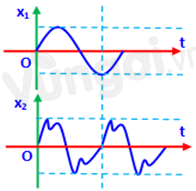
Biểu diễn trên đồ thị như sau:

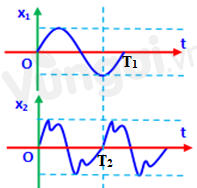
Từ đồ thị ta thấy: \({T_1} > {\rm{ }}{T_2} \Rightarrow {f_1} < {f_2}\)

Vậy độ cao của âm 2 lớn hơn âm 1.

Ta có:

Cường độ âm: \(I = \frac{P}{{4\pi {R^2}}} = \frac{{30}}{{4\pi {{.150}^2}}} = 1,{06.10^{ - 4}}{\rm{W}}/{m^2}\)

Công suất mà micro nhận được là:

\({P_{mic{\rm{r}}o}} = I.S' = 0,{8.10^{ - 8}}{\rm{W}}\)