Câu hỏi:
2 năm trước
Ba điểm O, A, B cùng nằm trên một nửa đường thẳng xuất phát từ O. Tại O đặt một nguồn điểm phát sóng âm đẳng hướng ra không gian, môi trường không hấp thụ âm. Mức cường độ âm tại A là 60dB, tại B là 20dB. Mức cường độ âm tại trung điểm M của đoạn AB là
Trả lời bởi giáo viên
Đáp án đúng: a
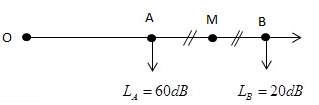
M là trung điểm của AB nên:
\(OM = \dfrac{{OA + OB}}{2} \Rightarrow {r_M} = \dfrac{{{r_A} + {r_B}}}{2}\)
Ta có: \(\left\{ \begin{array}{l}{L_A} = 10.\log \dfrac{P}{{4\pi r_A^2.{I_0}}} = 60dB\\{L_B} = 10.\log \dfrac{P}{{4\pi r_B^2.{I_0}}} = 20dB\\{L_M} = 10.\log \dfrac{P}{{4\pi r_M^2.{I_0}}}\end{array} \right.\)
\(\begin{array}{l} \Rightarrow {L_A} - {L_B} = 10.\log {\left( {\dfrac{{{r_B}}}{{{r_A}}}} \right)^2} = 20 \Rightarrow \log \dfrac{{{r_B}}}{{{r_A}}} = 2 \Rightarrow \dfrac{{{r_B}}}{{{r_A}}} = 100\\ \Rightarrow {r_M} = \dfrac{{{r_A} + 100{r_A}}}{2} = 50,5.{r_A}\end{array}\)
\(\begin{array}{l} \Rightarrow {L_A} - {L_M} = 10.\log {\left( {\dfrac{{{r_M}}}{{{r_A}}}} \right)^2}\\ \Leftrightarrow 60 - {L_M} = 10.\log 50,{5^2} \Rightarrow {L_M} \approx 26dB\end{array}\)
Hướng dẫn giải:
Công thức tính mức cường độ:
\(L = 10.\log \dfrac{I}{{{I_0}}} = 10.\log \dfrac{P}{{4\pi {r^2}.{I_0}}}\)
Với r là khoảng cách từ nguồn âm đến điểm khảo sát.
Câu hỏi khác
- Bài tập các đại lượng đặc trưng của sóng cơ học có đáp án MÔN LÝ lớp 12
- Bài tập lí thuyết về sóng cơ và sự truyền sóng cơ có đáp án MÔN LÝ lớp 12
- Bài tập lý thuyết chung về giao thoa sóng có lời giải MÔN LÝ lớp 12
- Bài tập đồ thị sóng cơ học có đáp án MÔN LÝ lớp 12
- Bài tập phương trình sóng cơ học có đáp án MÔN LÝ lớp 12
